Лекция. Таќырыбы:Векторлардың векторлық және аралас көбейтіндісі
Таќырыбы:Векторлардың векторлық және аралас көбейтіндісі. Векторлық және аралас көбейтіндіні координаталар арқылы өрнектеу.
1-анықтама. 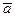 векторының
векторының 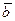 векторына векторлық көбейтіндісі деп, мынадай үш шартты қанағаттандырытын
векторына векторлық көбейтіндісі деп, мынадай үш шартты қанағаттандырытын 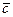 векторын айтады:
векторын айтады:
1. Вектор 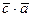 және
және 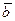 векторларына перпендикуляр, яғни
векторларына перпендикуляр, яғни 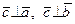 ;
;
2. Көбейтінді 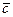 векторының ұзындығы көбейткіш
векторының ұзындығы көбейткіш 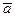 және
және 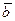 векторларда құралған параллелограмның ауданына тең, яғни
векторларда құралған параллелограмның ауданына тең, яғни 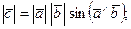
3. Көбейтінді 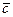 векторының ұшынан қарағанда бірінші көбейткіш
векторының ұшынан қарағанда бірінші көбейткіш 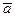 векторынан екінші көбейткіш
векторынан екінші көбейткіш 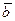 векторына қарай кіші бұрыш жасап айналу бағыты сағат тілінің бағытына қарсы орындалады (6.1-сурет).
векторына қарай кіші бұрыш жасап айналу бағыты сағат тілінің бағытына қарсы орындалады (6.1-сурет).
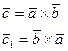








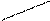




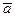
Сурет.
Екі вектордың векторлық көбейтіндісі 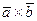 немесе
немесе 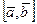 деп белгіленеді, яғни
деп белгіленеді, яғни 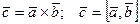 .
.
Векторлық көбейтіндінің қасиеттері.
10. 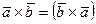 . Шынында,
. Шынында, 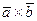 және
және 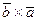 векторларының ұзындықтары бірдей және коллинеар болады, себебі
векторларының ұзындықтары бірдей және коллинеар болады, себебі 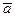 және
және 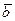 векторлары жатқан жазықтыққа перпендикуляр. Бағыттары қарама-қарсы (анықтама бойынша) (6.1-сурет).
векторлары жатқан жазықтыққа перпендикуляр. Бағыттары қарама-қарсы (анықтама бойынша) (6.1-сурет).
20. Егер 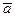 және
және 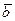 коллинеар векторлар болса, онда
коллинеар векторлар болса, онда 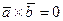 .
.
Шынында, егер 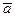 және
және 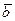 коллинеар векторлар болса, онда
коллинеар векторлар болса, онда 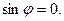 Сонда
Сонда 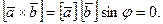 Демек,
Демек, 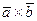 векторларының ұзындығы нөльге тең. Бұдан
векторларының ұзындығы нөльге тең. Бұдан 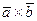 векторы нөль вектор екендігі шығады.
векторы нөль вектор екендігі шығады.
30. 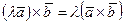 .
.
40. 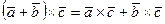 .
.
Теорема. Егер тік бұрышты координаттар системасында 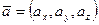 және
және 
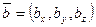 векторлары координаталары арқылы берілген болса, онда сол системадағы векторлық көбейтіндінің сызықтық жіктелуі мына түрде болады:
векторлары координаталары арқылы берілген болса, онда сол системадағы векторлық көбейтіндінің сызықтық жіктелуі мына түрде болады:
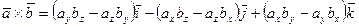 (6.1)
(6.1)
Бұл өрнекті символды түрде үшінші ретті анықтауыш арқылы былай жазады:
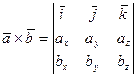 (6.2)
(6.2)
Анықтауышты бірінші жатық жолы бойынша жіктесек, төмендегіше болады:
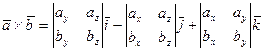
Дәлелдеуі. Базистік 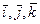 векторлардың анықтамасы бойынша және векторлық көбейтіндіні 10 және 30 қасиеттерін пайдалансақ, мынадай теңдіктерді аламыз:
векторлардың анықтамасы бойынша және векторлық көбейтіндіні 10 және 30 қасиеттерін пайдалансақ, мынадай теңдіктерді аламыз:
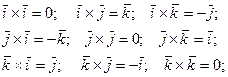
Енді 40 қасиетін және жоғарыдаға алынған теңдіктерді ескерсек (6.1) формуланы аламыз:
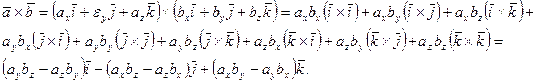
Екі векторлық көбейтіндісінің 20 қасиетін пайдалансақ, екі вектордың коллинеарлық шарты былай жазылады:
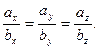
1-мысал. Төбелері 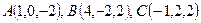 болатын үшбұрыштың ауданын және
болатын үшбұрыштың ауданын және 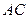 қабырғасына түсірілген биіктігінің ұзындығын есептеу керек (6.2-сурет).
қабырғасына түсірілген биіктігінің ұзындығын есептеу керек (6.2-сурет).


 в д
в д
hB
А Е С
Сурет.
Шешуі. 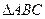 үшбұрышының ауданы
үшбұрышының ауданы 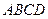 параллелограмның ауданының жартысына тең болғандықтан: ол үшбұрыштың ауданы
параллелограмның ауданының жартысына тең болғандықтан: ол үшбұрыштың ауданы 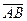 және
және 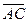 векторларының векторлық көбейтіндісінің модулінің жартысына тең болады:
векторларының векторлық көбейтіндісінің модулінің жартысына тең болады:


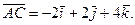
Бұл векторлардың векторлық көбейтіндісін (12) формула бойынша есептейміз.
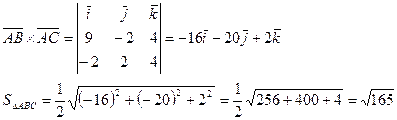
Үшбұрыштың ауданын 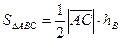 формуласына
формуласына 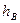 биіктігін табамыз:
биіктігін табамыз:
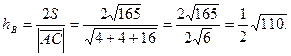
2-мысал. 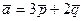 және
және 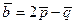 векторлары берілген. Мұнда
векторлары берілген. Мұнда 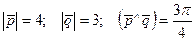 .
. 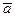 мен
мен 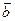 векторлары арқылы тұрғызылған параллелограмның ауданын табу керек.
векторлары арқылы тұрғызылған параллелограмның ауданын табу керек.
Шешуі. Векторлық көбейтіндінің анықтамасын және қасиеттерін пайдаланамыз:
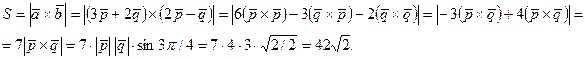 3-мысал.
3-мысал. 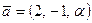 және
және 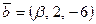 векторлары
векторлары  мен
мен 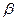 қандай мәндерінде коолинеар болады?
қандай мәндерінде коолинеар болады?
Шешуі. Екі вектор коллинеар боу үшін оның сәйкес координаталары пропоционал болуы қажет: 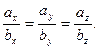
Демек, 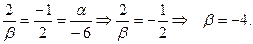
Дәл сол сияқты 
4-мысал. Егер 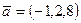 және
және 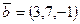 болса, онда
болса, онда 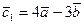 және
және 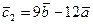 векторлары коллинеар бола ма?
векторлары коллинеар бола ма?
Шешуі. 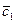 және
және 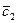 векторларының координатасын берілген амалдарды орындап табайық:
векторларының координатасын берілген амалдарды орындап табайық:
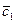 =4(-1, 2, 8)-3(3, 7, 1)=(-4, 8, 32)-(9, 21, -3)=(-13, -13, 36),
=4(-1, 2, 8)-3(3, 7, 1)=(-4, 8, 32)-(9, 21, -3)=(-13, -13, 36),
 9(3, 7, -1)-12(-1, 2, 8)=(37, 63, -9)-(-12, 24, 96)=(39, 39, -105).
9(3, 7, -1)-12(-1, 2, 8)=(37, 63, -9)-(-12, 24, 96)=(39, 39, -105).
Сәйкес координаталары  пропоционал болғандықтан
пропоционал болғандықтан 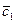 және
және 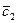 векторлары өзара коллинеар.
векторлары өзара коллинеар.
Үш вектор бойынша сипаты әртүрлі бірнеше көбейтінділер құруға болады.
1. Екі вектор скаляр көбейтіліп, одан шыққан скаляр үшінші векторға көбейтіледі. Егер көбейткіш векторлар  болса, онда мұндай көбейтінді былай белгіленеді:
болса, онда мұндай көбейтінді былай белгіленеді: 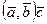 . Көбейтіндінің нәтижесінде
. Көбейтіндінің нәтижесінде 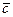 векторына коллинеар вектор шығады.
векторына коллинеар вектор шығады.
2. Үш вектордың аралас көбейтіндісі. Үш вектордың аралас көбейтіндісі деп, екі вектордың векторлық көбейтіндісі үшінші векторға скаляр көбейткенде айтады.
Егер көбейткіш векторлар  болса, аралас көбейтінді
болса, аралас көбейтінді 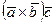 немесе
немесе  түрінде жазылады. Аралас көбейтіндінің нәтижесі скаляр шама болады, оның абсолют шамасы берілген үш вектордан құралған параллелепипедтың көлеміне тең, яғни
түрінде жазылады. Аралас көбейтіндінің нәтижесі скаляр шама болады, оның абсолют шамасы берілген үш вектордан құралған параллелепипедтың көлеміне тең, яғни 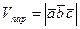 .
.
Егер үш көбейткіш вектор оң система құрса, онда аралас көбейтіндінің нәтижесі оң сан, ал егер сол система құрса, нәтижесінде теріс сан болады.
Аралас көбейтіндінің қасиеттері:
10. 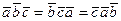
20. 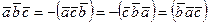
30. Егер 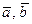 және
және 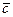 векторлары коллинеар болса, онда
векторлары коллинеар болса, онда 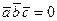 .
.
Теорема. Тікбұрышты координаттар системасында 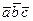 векторларының координаталары белгілі болса, онда олардың аралас көбейтіндісі сол векторлардың координаталарынан құралған үшінші ретті анықтауышқа тең болады:
векторларының координаталары белгілі болса, онда олардың аралас көбейтіндісі сол векторлардың координаталарынан құралған үшінші ретті анықтауышқа тең болады:
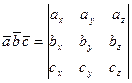 .
.
Дәлелдеуі.  болғандықтан, екі вектордың векторлық көбейтіндісі бойынша:
болғандықтан, екі вектордың векторлық көбейтіндісі бойынша:
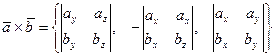 .
.
Енді 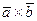 векторын
векторын 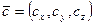 векторына скаляр көбейтсек:
векторына скаляр көбейтсек:
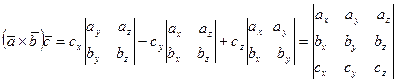 .
.
3.Үш вектордың екі еселі векторлық көбейтіндісі. Үш вектордың екі еселі векторлық көбейтіндісі деп, екі вектордың векторлық көбейтіндісін үшінші векторға векторлық көбейткенді айтады да, былай белгілейді 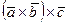 .
.
Екі еселі векторлық көбейтіндіні табу үшін, оны үш вектордың көбейтіндісінің бірінші түріне келтіру формулаларын пайдаланады, яғни
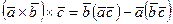 немесе
немесе 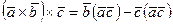
1-мысал. 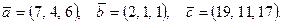 векторлары өзара компланар ма, жоқ па?
векторлары өзара компланар ма, жоқ па?
Шешуі. Үш вектордың компланарлығының шарты олардың аралас көбейтіндісінің нөльге тең болуы:
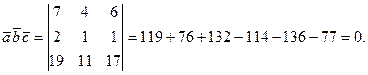
Демек, берілген векторлар компланар екен.
2-мысал. 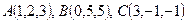 және
және 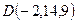 нүктелері бір жазықтықта жата ма?
нүктелері бір жазықтықта жата ма?
Шешуі: 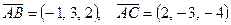 және
және 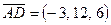 векторларын қарастырамыз.
векторларын қарастырамыз. 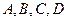 нүктелерінің бір жазықтықта жату шарты
нүктелерінің бір жазықтықта жату шарты 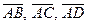 векторларына компланар болу шартымен бірдей. Сондықтан
векторларына компланар болу шартымен бірдей. Сондықтан 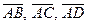 векторларының аралас көбейтіндісін есептейік:
векторларының аралас көбейтіндісін есептейік:
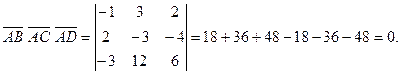
Демек, 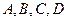 нүктелері бір жазықтықта жатыр.
нүктелері бір жазықтықта жатыр.
3-мысал. 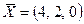 векторын мүмкін болса
векторын мүмкін болса 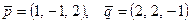 және
және 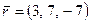 векторлары бойынша жіктеу керек.
векторлары бойынша жіктеу керек.
Шешуі: 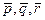 кеңістікте базис құрайтын болса, онда есептің шешімі болады. Бұл векторлар базис құру үшін олардың компланар болмауы керек. Сондықтан ол векторлардың аралас көбейтіндісін есептейік:
кеңістікте базис құрайтын болса, онда есептің шешімі болады. Бұл векторлар базис құру үшін олардың компланар болмауы керек. Сондықтан ол векторлардың аралас көбейтіндісін есептейік:
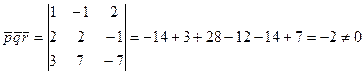 .
.
Демек, 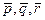 векторлары базис құрайды. Сондықтан
векторлары базис құрайды. Сондықтан 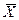 векторын
векторын 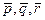 векторларлары бойынша жіктеуге болады, яғни
векторларлары бойынша жіктеуге болады, яғни 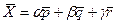 болатындай
болатындай  сандарын табуға болады. Соңғы теңдікті координаталар түрінде жазсақ
сандарын табуға болады. Соңғы теңдікті координаталар түрінде жазсақ 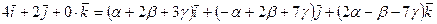 болады.
болады.
Бұдан мынадай теңдеулер системасын аламыз:
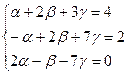
Бұл теңдеулер системасын Крамер формуласын пайдаланып шешейік:
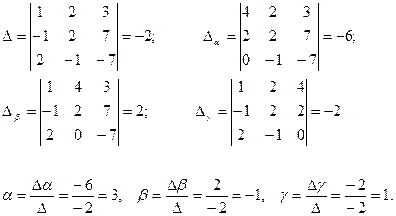
Демек, 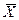 векторы
векторы 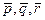 векторлары бойынша былай жіктеледі:
векторлары бойынша былай жіктеледі:
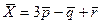 .
.
4-мысал. Төбелері А1(1, -1, 2), А2(2, 1, 2), А3(1, 1, 4) және А4(6, -3, 6) нүктелері болатын тетраэдрдің көлемін және А4 нүктесінен А1А2А3 жағына түсіретін биіктігін табу керек.
Шешуі. Тетраэдрдің 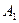 төбесінен шығатын
төбесінен шығатын 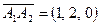 ,
, 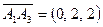 ,
, 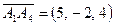 векторларын қарастырамыз. Бұл векторлардың аралас көбейтіндісін геометриялық мағынасы бойынша
векторларын қарастырамыз. Бұл векторлардың аралас көбейтіндісін геометриялық мағынасы бойынша 
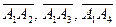 векторлары арқылы құралған параллелепипед көлемін табамыз:
векторлары арқылы құралған параллелепипед көлемін табамыз:
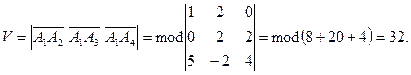
Сонда тетраэдрдің көлемі 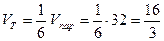 .
.
Екінші жағынан 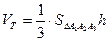 . Сонда
. Сонда 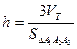 .
. 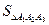 -ді табу үшін
-ді табу үшін 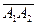 және
және 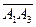 векторларын қарастырамыз. Екі вектордың векторлық көбейтіндісінің геометриялық мағынасы бойынша:
векторларын қарастырамыз. Екі вектордың векторлық көбейтіндісінің геометриялық мағынасы бойынша:
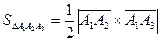 .
.
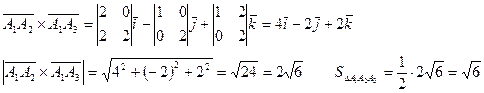
Демек, 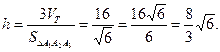
Дата добавления: 2015-08-20; просмотров: 7247;
