Сурет. 1.8-сурет.

Векторды нақты санға көбейту үшін келесі қасиеттерге сүйенеміз:

а). 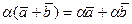. (векторлар қосындысы бойынша үлесімділік заңы);

ә). 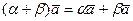. (сандар көбейтіндісі бойынша үлесімділік заңы);

б). 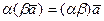. (сандар көбейтіндісі бойынша терімділік заңы);

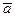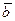Жоғарыдағы а) қасиетті дәлелдеу үшін «параллеограмм ережесің бойынша және векторларының қосындысын саламыз. Енді векторды санға көбейту анықтамасы бойынша, әр көбейтінді есе өседі, онда параллелограмм диагоналі де сонша еесге ұзарады (1.8-сурет). Векторлар колинеары болған кезде және <0 болғанда анықтамаларға сүйеніп оңай көз жеткізуге болады. Векторды санға көбейтудің келесі 2) және 3) қасиеттерін дәлелдеу онша қиынға түспейді. Сондықтан да, оларды келтірмеуді жөн көрдік.

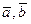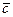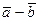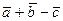Мысал. Берілген және векторлары бойынша (1.9-сурет) тізбектеп қосу немесе «үшбұрыштарң және «параллелограммң ережелерін пайдаланып а) ; ә) ; б) 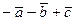векторларын салайық.

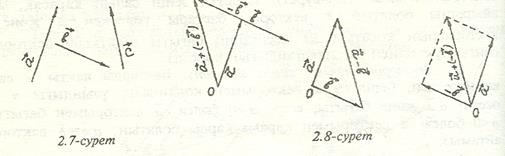
Шешуі: Тізбектеп қосу немесе «үшбұрыштарң және «параллелограммң ережелерін қолданып жеке-жеке 1), 2), 3) векторлары салынып, дұрыстығына көз жеткізу үшін біріктііріліп, сәйкес (1.10; 1.11; 1.12 суреттерде) көрсетілген.