Лекция. Таќырыбы: Кеңістіктегі координаталар жүйесі

Таќырыбы: Кеңістіктегі координаталар жүйесі. Кеңістіктегі аналитикалық геометрияның қарапайым есептері.

Кеңістікте үш координаталық ось өзара тікбұрыш жасап қиылысын. Олардың өлшем бірліктері (масштабтары) бірдей болсын. Олардың ортақ қиылысу нүктесін О - мен белгілеп координаталар басы деп атаймыз. Алынған жүйені кеңістіктегі тік Декарттық координаталар жүйесі деп атаймыз (1 – сызба).

Бірінші координаталық осьті х әріпімен белгілейміз. Ох осі немесе абсцисса осі деп атаймыз.

Екінші координаталық осьті y әріпімен белгілейміз. Оy осі немесе ордината осі деп атаймыз.

Үшінші координаталық осьті z әріпімен белгілейміз. Оz осі немесе аппликата осі деп атаймыз.

Кеңісітіктегі тік Декартты координаталар жүйесі кеңістікті сегіз бөлікке бөледі. Оларды октанта деп атаймыз (2 -сызба).

І октанта х > 0, y > 0, z > 0

ІІ октанта х < 0, y > 0, z > 0

ІІІ октанта х < 0, y < 0, z > 0

ІҮ октанта х > 0, y < 0, z > 0

Ү октанта х > 0, y > 0, z < 0

ҮІ октанта х < 0, y > 0, z < 0

ҮІІ октанта х < 0, y < 0, z < 0

ҮІІІ октанта х > 0, y < 0, z < 0

Кеңістікте кез- келген М (х, y, z) нүктесі берілсін. Ол жазықтық z осін бір нүктеде қияды. Ол нүктені Мz нүктесі деп белгілейміз. Тура сол сияқты М нүктесінен хОz және yОz осьтеріне параллель түзу жүргізейк. Олар сәйкесінше y осінен және х осінен Мy, Мz нүктесін қиып өтеді (3 сызба). Онда ОМх, ОМy, ОМz шамаларын М нүктесінің кеңістіктегі тік Декарттық координатасы деп атаймыз және келесі символмен беогілейміз – М(х, y, z). Мұндағы х = ОМх, y = ОМy, z = ОМz.

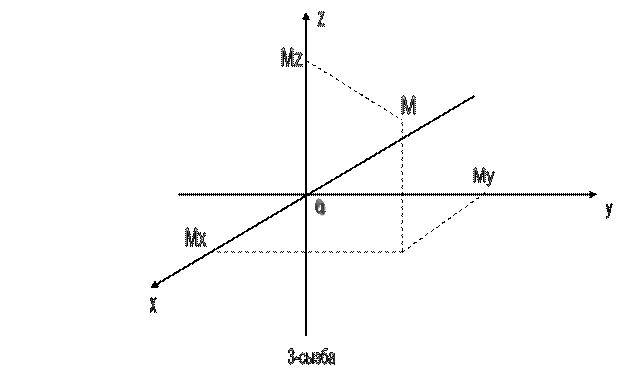
Кеңістіктегі тік Декарттық координаталар үшін М₁ (х₁, y₁, z₁) және М₂ (х₂, y₂, z₂) нүктелерінің арақашықтығы

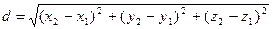(1)

формуласымен анықталады.

Кеңістіктегі М₁ (х₁, y₁, z₁), М₂ (х₂, y₂, z₂), М₃ (х₃, y₃, z₃) нүктелері берілсін және М (х, y, z) нүктесі М₁ М₂ кесіндісін λ қатынасына бөлінсін, онда

λ = М₁ М / М М₂ – формуласымен анықталады. Соған байланысты М нүктесінінң координаталары мына формулалар арқылы анықталады:

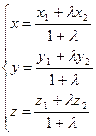(2)

Кесіндіні берілген қатынастар бөлу формуласы.

Егер λ = 1 болса, онда кесінді қақ бөлінеді.

(3)

Цилиндрлік координаталар жүйесі.

Кеңістікте тік декарттық коодинаталардан басқа цилиндрлік координаталарда еңгізіледі. Цилиндрлік координаталар хОy жазықтығына полярлық координаталарды енгізу арқылы анықталады. Ал z осі өзгеріссіз қалады. Сонда кеңістіктегі кез-келген нүкте ρ, α, z шамалары арқылы бір мәнді анықталады.

ρ, α, z кеңістіктегі нүктенің полярлық координаталары деп аталады. Кеңістікте кез-келген М (ρ, α, z) цилиндрлік координаталар арқылы берілсін. Онда кеңістікте М нүктесі келесі түрде анықталады. Кеңістікте О нүктесімен (полюс) және х сәулесі (поляр) центры О нүктесінде радиусы ρ –ға тең шеңбер жүргізейік (4 сызба).

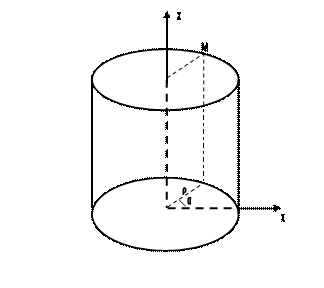
Кеңістіктегі тік декарттық координаталарда цилиндрлік координаталарда кеңістіктің кез-келген нүктесінің бір мәнді анықтағандықтан олардың арасында белгілі бір байланыс болуы керек. Сол байланысты анықтайық.

Кеңістікте цилиндрлік координаталарды енгізу үшін хОy жазықтығына полярлық координаталар енгізілетіндіктен, ал z осін өзгеріссіз қалдырғандықтан:

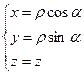(4).

Сфералық координаталар жүйесі.

Кеңістікте тік Декарттық координаталардан басқа сфералық координаталарда енгізіледі. Кеңістіктегі сфералық координаталар ρ, α, θ шамалары арқылы бір мәнді анықталады. Мұндағы

ρ – координаталар басынан кеңістіктегі кез-келген нүктеге дейінгі арақашықтық

θ – ρ арақашықтықтан z осі арасындағы L

α – нүктенің хОy жазықтығына проекциясының х осімен арасындағы бұрышы.

Кеңістікте кез-келген М (ρ,α,θ) нүктесі арқылы берілсін. Онда ол келесі түрде анықталады. Кеңістікте кез-келген нүктемен одан шығатын сәуле алайық. Центрі О нүктесінде, радиусы О-ға шеңбер жүргізейік. Х осімен α ^Ә бұрыш жасайтын нүкте алайық. Табылған нүктені О нүктесімен қосайық. Шыққан сәуле шеңберді бір нүктеде қияды. Оны Р әрпімен белгілейік. Бірінші шеңберге перпендикуляр болатын z осін алайық. Центрі О нүктесінде, радиусы ρ –ға тең. Р нүктесінен өтетін және z осін қиып өтетін екінші шеңбер жүргізейік. Екінші шеңбер ойымы z осімен 0Ә бұрышы жасайтын нүкте алайық, табылған нүктені координаталар басымен қосайық. Шыққан сәуле екінші шеңберді бір нүктеде қияды. Ол ізделінді М нүктесі (5 сызба).

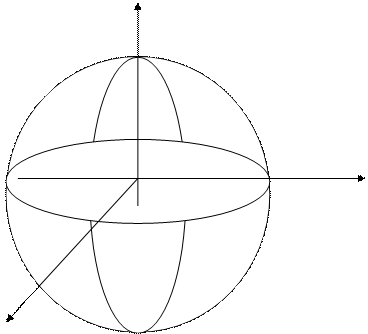Z

y

х

5- сызба

Кеңістіктегі кез-келген тік Декартық координаталарда да сфералық координаталарда да кеңістіктіктің кез-келген нүктесінің бір-мәнін анықтағанда олардың арасында байланыс болады.

Х / ОMyх = cos α

x = OMxy Һ cos α = ρ sіn θ Һ cos α

y = OMxy Һ sіn α = ρ sіn θ Һ sіn α

x = ρ cos α Һ sіn θ

y = ρ sіn α Һ sіn θ

z = ρ cos θ (5)

Сфералық координаталардан декарттық координаталарға көшу формуласы.