Определение абстрактного цифрового автомата
Обобщённая структура системы обработки цифровой информации, приведённая на рис.1, соответствует описанию абстрактного цифрового автомата. Для целей технического проектирования в каноническую структурную систему цифрового автомата необходимо включить систему синхронизации или систему задания автоматного времени. Введение системы автоматного времени обеспечивает устойчивость работы технического устройства - цифрового автомата и дискретный характер временных процессов в нём.
С помощью импульсов синхронизации исключается возможность некорректной работы цифрового автомата во время протекания переходных процессов в элементах блока памяти и в комбинационных схемах. Цифровые автоматы, работающие под управлением системы задания дискретного автоматного времени, называются синхронизированными цифровыми автоматами. Наличие системы задания дискретного автоматного времени накладывает ограничения и на порядок изменения входных управляющих сигналов множества X. Поскольку сигналы множества X формируются в других блоках сложной информационной системы, то учёт ограничений системы задания дискретного времени приводит к практической необходимости включения в информационную систему любой сложности единой системы синхронизации.
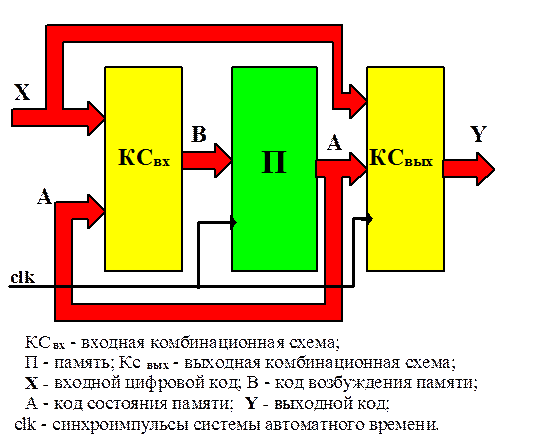
Для абстрактного математического описания цифрового автомата как кодопреобразователя (рис.1) используется его представление как шестиэлементного множества:
S ={A, X ,Y, d, l, a1}, (32)
где: A = {a1, .., am, ..., aM} - множество состояний автомата (алфавит состояний); X = {z1, ..., zf, ..., zF} - множество входных сигналов автомата (входной алфавит); Y = {w1, ..., wg, ..., wG} - множество выходных сигналов (выходной алфавит);
d - функция переходов абстрактного цифрового автомата, реализующая отображение множества Dd в A (Dd является подмножеством прямого произведения множеств A´X, то есть Dd Í A´X). Таким образом, любое состояние цифрового автомата as = d(am, zf), поскольку множество A´X является множеством всевозможных пар (a, z) и as Î A.
l - функция выходов абстрактного цифрового автомата, реализующая отображение множества Dl в Y (Dl является подмножеством прямого произведения множеств A´X, то есть Dl Í A´X). Таким образом, любой выходной сигнал множества Y wg = l(am, zf);
a1 - начальное состояние автомата (a1 Î A). Поведение цифрового автомата существенно зависит от начального состояния. Для однозначного управления цифровым автоматом необходимо, чтобы он начинал работу из определённого начального состояния. Цифровой автомат с установленным (выделенным) начальным состоянием a1 называется инициальным.
Автомат является конечным, если A, X и Y - не являются бесконечными множествами.
Автомат является полностью определённым, если Dd = Dl = A´X. Иными словами, у полностью определённого автомата области определения функций d и l совпадают с множеством A´X - множеством всевозможных пар (am, zf). У частичного автомата функции d и l определены не для всех пар (am, zf) Í A´X.
Теоретически все элементы множеств A, X ,Y могут быть закодированы числами в системах счисления с любым основанием, но практически всегда используется двоичная система счисления (двоичный структурный алфавит).
Для двоичной системы счисления обозначим:
A = {a1, .., am, ..., aM}, X = {x1, ...,xf, ...,xF}, Y = {y1, ..., yg, ...,yG} и определим разрядность двоичных кодов состояний, входного сигнала и выходного сигнала. Количество разрядов двоичного кода всегда целое число.
Количество разрядов двоичного кода состояний
p = ]log2M[. (33)
Количество разрядов двоичного кода входных сигналов
r = ]log2F[. (34)
Количество разрядов двоичного кода выходных сигналов
d = ]log2G[. (35)
В этих формулах ]...[ - означает ближайшее большее к значению внутреннего выражения целое число.
Согласно структурной схеме рис.21 коды наборов переменных комбинационных схем определяются в результате конкатенации кодов входных сигналов и кодов состояний блока памяти. Как наборы входных переменных, так и коды состояний блока памяти содержат запрещённые комбинации и поэтому системы функций алгебры логики, описывающих комбинационные схемы, будут не полностью определёнными.
Максимально возможное количество запрещённых кодов наборов переменных комбинационных схем определится как:
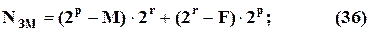
В зависимости от схемы кодирования входных сигналов и состояний, среди этих запрещённых наборов могут оказаться одинаковые, и поэтому реально количество запрещённых наборов на число совпадающих кодов меньше, чем определённое по ф.(36).
Часто на практике используется две разновидности цифровых автоматов, отличающихся способом формирования выходных сигналов:
- при описании функционирования автомата выражениями:
a(t+1) = d[a(t), z(t)],
w(t) = l[a(t), z(t)] - он называется автоматом Мили;
- при описании функционирования автомата выражениями:
a(t+1) = d[a(t), z(t)],
w(t) = l[a(t)] - он называется автоматом Мура.
В этих выражениях t - текущий момент дискретного автоматного времени, t+1 - следующий момент дискретного автоматного времени.
Дата добавления: 2015-08-20; просмотров: 899;
