ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ И АППАРАТЫ
Раздел 1. ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ
И АППАРАТЫ 38ч., в т.ч. лаб. раб. и практ. занят 22ч.
Тема 1.1. Общие вопросы прикладной гидромеханики 12ч., в т.ч. лаб. раб. и практ. занят 8ч.
Студент должен:
знать:
- зависимость свойств жидкостей от давления, температуры;
- сущность гидростатического, абсолютного и избыточного давления;
- уравнения расхода и материального баланса потока;
- уравнение энергетического баланса;
- потери напора и давления при движении жидкости;
- порядок расчетов трубопроводов;
уметь:
- определять по справочнику свойства жидкостей в зависимости от условий;
- определять давление в назначенных точках систем;
- рассчитывать режим движения жидкостей;
- определять потери давления и напора;
- определять основные расходные характеристики, диаметр трубопровода;
- рассчитывать гидравлическое сопротивление зернистого слоя.
Реальные и идеальные жидкости. Физические свойства и параметры реальной жидкости. Гидростатика. Гидростатическое давление и его свойства. Гидродинамика. Уравнение материального баланса. Энергетический баланс потока. Уравнение Бернулли. Основные критерии гидродинамического подобия. Гидродинамические режимы вязкой жидкости. Гидродинамические сопротивления трубопроводов и аппаратов. Движение жидкости через неподвижные, пористые и зернистые слои. Гидродинамика псевдоожиженного слоя.
ОБЩИЕ ВОПРОСЫ ПРИКЛАДНОЙ ГИДРОМЕХАНИКИ
Гидромеханика – раздел механики сплошных сред, изучающий законы равновесия (гидростатика) и движения (гидродинамика) жидкостей и газов, а также механическое взаимодействие между жидкостью и твердыми телами (стенками), омываемыми ею. В отличие от твердых тел жидкости и газы обладают свойствами текучести, т. е. даже очень малые силовые воздействия вызывают их деформацию.
Прикладная гидромеханика, или гидравлика, - техническая наука, представляющая собой механику жидкости, в которой широко используются обоснованные допущения и предположения, упрощающие рассмотрение процессов. В гидравлике широко используют экспериментальные данные, которые позволяют решать сравнительно сложные практические задачи механики жидкости.
С этой целью в гидромеханике вводится понятие идеальной жидкости, которая в отличие от реальной (вязкой) жидкости абсолютно несжимаема, т. е. не меняет плотность при изменении давления и температуры, а также не обладает внутренним трением между ее слоями (вязкостью).
В свою очередь реальные жидкости делятся на капельные (жидкости) и упругие (газы и пары), причем, если первые практически несжимаемы и обладают малым коэффициентом объемного расширения, объем последних значительно изменяется при изменении температуры и давления.
К основным физическим величинам, характеризующим Свойства рассматриваемых сред, относятся:
плотность (ρ, кг/м3), определяемая в случае однородного тела отношением
ρ=m/V,
где m - масса тела; V- его объем;
удельный вес (γ, Н/мз), определяемый для однородного тела отношением
γ= G/V,
где G – вес тела.
Поскольку вес тела и его масса связаны соотношением
G = mg,
где g – ускорение свободного падения (на поверхности Земли g = 9,81 м/с2), плотность тела является величиной постоянной, а удельный вес того же тела - величиной переменной в зависимости от значения ускорения свободного падения.
Плотность и удельный вес капельных жидкостей значительно больше, чем соответствующие характеристики упругих жидкостей (газов);
· давление (р, Н/м2), определяемое выражением
P = P/F
где Р – сила, действующая на поверхность F перпендикулярно к ней.
Поскольку упругие жидкости обладают сжимаемостью, их плотность в значительной степени зависит от давления и температуры. Связь между ними может быть определена уравнением состояния

где V – объем газа, м3; m – масса газа, кг; R = 8,31*103 Дж/(кмоль*град) – универсальная газовая постоянная; Т – температура, К; М – молекулярная масса газа, кг/кмоль.
Из уравнения (1.1) следует, что плотность упругих жидкостей определяется зависимостью
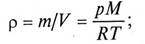
· вязкость молекулярная (физическая) – свойство реальной жидкости оказывать сопротивление движению в результате возникновения сил внутреннего трения.
При течении реальной жидкости скорость соседних слоев различается на величину dw. Таким образом, для перемещения одного слоя относительно другого необходимо приложить некоторую силу Т, которая, отнесенная к поверхности перемещаемых слоев F, позволяет получить характерный для рассматриваемой жидкости параметр, называемый напряжением внутреннего трения τ,
τ = Т/F.
Согласно закону Ньютона – Петрова

где dw/dn – градиент скорости, характеризующий изменение скорости по нормали между слоями.
Коэффициент пропорциональности (µ, Па*с) в уравнении (1.2) называется динамической вязкостью (иногда его называют коэффициентом вязкости, коэффициентом внутреннего трения).
Величину, равную отношению динамической вязкости к плотности среды, называют кинематической вязкостью (ν, м2/с)
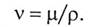
Вязкость капельных жидкостей снижается с увеличением температуры, в отличии от вязкости газов, которая увеличивается с ее повышением;
· поверхностное натяжение (коэффициент поверхностного натяжения) (б, Н/м) определяется как отношение силы Р, действующей на участок контура поверхности жидкости, к длине l этого участка:
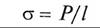
и определяет формирование поверхности на границе раздела жидкость – газ (пар) или жидкость – жидкость (несмешиваемые друг с другом).
Значения величин плотностей, вязкостей и поверхностного
натяжения для различных сред и условий можно найти в специальной справочной литературе.
Гидростатика – раздел гидромеханики, в котором изучается состояние жидкостей, находящихся в относительном покое или условиях равновесия, когда частицы и слои, составляющие их, не перемещаются друг относительно друга. Поскольку при этом внутренние силы (трения) отсутствуют, а рассматриваются только внешние силы (тяжести, давления), жидкость близка к идеальной.
Давление жидкости Р на единицу поверхности F называется гидростатическим давлением (р, Н/м2) и определяется соотношением
Однако истинное гидростатическое давление – это давление в точке, которое определяется как
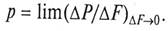
К основным свойствам гидростатического давления можно отнести следующие:
· гидростатическое давление определяется весом столба жидкости высотой h над рассматриваемым участком:
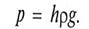
Если давление над жидкостью равно ро, то
Р = ро + hρg;
· гидростатическое давление всегда направлено от жидкости к воспринимающей поверхности по перпендикуляру;
· величина гидростатического давления на одном уровне жидкости одинакова по всем направлениям.
Гидродинамика – раздел гидромехани ки, в котором рассматриваются задачи, связанные с движением жидкости под действием приложенных к ней внешних сил – разности давлений, создаваемой с помощью н агнетательного оборудования (насосов или компрессоров), либо вследствие разности уровней или плотностей жидкостей.
При рассмотрении течения жидкости по запол ненному трубопроводу различают:
· линейную скорость w – путь, пройденный количеством жидкости в единицу времени.
В связи с тем, что скорость отдельных слоев жидкости неодинакова, чаще рассматривают среднюю скорость потока (w, м/с)
w = V/F (1.3)
где V – объемный расход потока; F – площадь поперечного сечения трубопровода;
· объемный расход потока (V, м3/с), определяемый по уравнению, обратному (1.3),
V = wF;
· массовую скорость (W, кг/(м2*с)), определяемую как количество жидкости, перемещенное через единицу поперечного сечения в единицу времени,
W = G/F = wρ, (1.4)
где G = Wρ — массовый расход жидкости.
В случае установившегося (стационарного) движения, когда все параметры, характеризующие состояние системы в каждом сечении (скорость, расход, температура, плотность и др.), не меняются во времени, при переходе от сечения F1 к сечению F2 скорости жидкости w1 и w2 будут различны, однако по закону сохранения вещества массовый расход жидкости, проходящей через каждое сечение, должен быть неизменен.
Таким образом, в соответствии с уравнением (1.4)
G = F1*w1*ρ1 = F2*w2*ρ2 = const. (1.5)
Считая жидкость несжимаемой (ρ1 = ρ2) уравнение (1.5) можно записать
V= F1*w1 = F2*w2 = const. (1.6)
Уравнения (1.5) и (1.6) называются уравнениями неразрывности потока и представляют собой материальный баланс потока жидкости.
Любая жидкость, находящаяся в состоянии относительного покоя или движения, обладает запасом энергии, равным сумме внутренней, потенциальной и кинетической энергии.
Внутренняя энергия U представляет собой суммарную энергию молекул жидкости, величина которой определяется многими параметрами – в частности температурой, с увеличением которой она возрастает.
Потенциальная энергия является суммой потенциальной энергии давления рV и потенциальной энергии положения mgz. Последняя определяется высотой центра тяжести г рассматриваемого объема жидкости над некоторой произвольно выбранной горизонтальной плоскостью (плоскостью сравнения).
Кинетическая энергия объема жидкости массой т, движущейся со скоростью w, определяется выражением m*w2/2.
Таким образом, полная энергия жидкости Е, равная сумме перечисленных энергий, составит
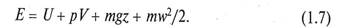
Обозначив сумму внутренней и потенциальной энергии давления
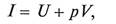
называемой энтальпией (теплосодержанием) потока, запишем уравнение (1.7) как

Удельная энергия е, приходящаяся на 1 кг жидкости, может быть представлена делением уравнений (1.7) и (1.8) на m:
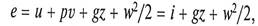
где u – внутренняя энергия 1 кг жидкости; v -объем, занимаемый 1 кг жидкости; i - энтальпия 1 кг жидкости.
В случае установившегося (стационарного) движения Жидкости по трубопроводу переменного сечения (рис. 1.1) без дополнительного подвода или отвода энергии ее удельная энергия по закону сохранения изменяться не будет. Поэтому при перемещении жидкости от некоторого сечения 1 – 1 до сечения 2 – 2, удельная энергия жидкости в них также не меняется:
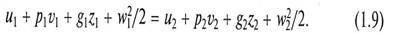
Поскольку v = 1/ρ, уравнение (1.9) можно представить в виде
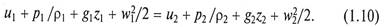
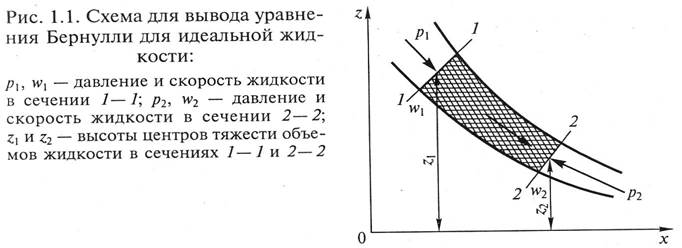
Учитывая, что для идеальной жидкости ρ1 = ρ2 = ρ (условие несжимаемости), u1= u2 (отсутствие внутреннего трения), уравнение (1.10) запишем как
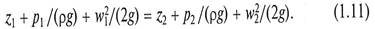
Данное уравнение, записанное в общем виде
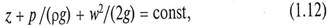
называется уравнением Бернулли для идеальной жидкости, а сумма в левой части – гидродинамическим напором.
При записи уравнения Бернулли для реальной жидкости необходимо учитывать изменение внутренней энергии системы между сечениями 1 – 1 и 2 – 2 введением в правую часть уравнения (1.11) слагаемого (u1- u2)/g:
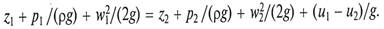
Дата добавления: 2015-08-14; просмотров: 2314;
