Отражение и прохождение волн на границах сред.
При падении упругих волн на границу раздела двух сред волны частично проходят во вторую среду, а частично отражаются. Коэффициент отражения R определяется как амплитуда Аотр - отраженной волны, деленная на амплитуду Апад - падающей волны:
R = Аотр / Апад.
Коэффициент прозрачности D – это отношение амплитуд для прошедшей и падающей волн: D = Апр / Апад.
Так же определяются коэффициенты отражения и прозрачности по энергии. Вместо амплитуд в формулы входят энергии волн.
Чем больше разница волновых сопротивлений сред (произведений плотности среды на скорость звука в ней), тем меньше доля прошедшей энергии и больше – отраженной. Например, при падении волны на границу сталь - воздух (или воздух - сталь) проходит только 0,002% энергии, через границу сталь – вода проходит около 12% энергии, а оргстекло – сталь – 25% (отражается – 75%). Это объясняется тем, что волновое сопротивление воды больше, чем воздуха, а оргстекла – еще больше. Они последовательно приближаются к волновому сопротивлению стали. Цифры приведены для продольной волны, перпендикулярно падающей на границу (рис. 2.11, а).
Если волны проходят из одной твердой среды в другую через зазор, заполненный воздухом, то прохождение очень плохое, так как для газов волновое сопротивление в тысячи раз меньше, чем для твердых тел. Это обеспечивает хорошее обнаружение очень тонких несплошностей (дефектов) в твердом теле: УЗ волны от них хорошо отражаются. Но это же затрудняет передачу УЗ волн от преобразователя, который их возбуждает и принимает, в объект контроля.
Для передачи УЗ колебаний от преобразователя в изделие зазор между ними заполняют жидкостью – контактной средой. Если жидкость полностью заполняет зазор и слой ее тонкий, то прохождение ультразвука вполне удовлетворительное.
При наклонном падении упругих волн на границу раздела двух сред происходит их отражение и преломление, также как для оптических волн (света). Угол отражения g (для волны того же типа) равен углу падения b. а угол преломления a определяется из закона: 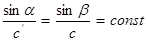 (то есть равно постоянной величине), где с' и с – скорость звука в первой и второй средах. Это соотношение называют законом Снеллиуса или законом синусов.
(то есть равно постоянной величине), где с' и с – скорость звука в первой и второй средах. Это соотношение называют законом Снеллиуса или законом синусов.
Если одна среда (или обе) – твердое тел, то в ней при падении упругой волны на границу возникает сразу две волны – продольная и поперечная. Явление превращения одного типа волн в другой называют трансформацией волн. Закон Снеллиуса остается справедливым для всех образовавшихся волн.
В УЗ контроле чаще всего встречается случай, когда падает продольная волна, а в результате преломления возникают продольная и поперечная волны, причем скорость обеих волн больше, чем падающей волны (рис. 2.11, б). Возникают также отраженные волны: продольная, если верхняя среда жидкая, продольная и поперечная, если верхняя среда твердая, как на рис. 2.11.
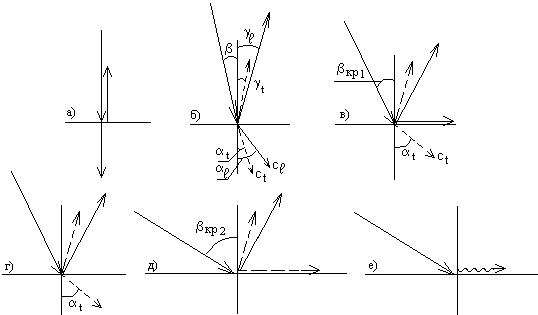 |
Будем увеличивать угол падения; тогда при некотором значении угла падения угол преломления для продольной волны будет равен 90° (рис. 2.11, в). Преломленная продольная волна будет распространяться вдоль поверхности. Она станет головной волной. Этот угол падения называют первым критическим. При больших углах падения (рис. 2.11, г) во второй среде останется только поперечная волна. При втором критическом угле (рис. 2.11, д) поперечная волна пойдет вдоль поверхности, т. е. обе преломленные волны испытают полное внутреннее отражение.
Рис. 2.11. Отражение, преломление и трансформация волн при падении продольной волны на границу оргстекло – сталь: сплошные линии – продольные волны, штриховые – поперечные волны, волнистая линия – поверхностная волна.
Критические углы рассчитываются по формуле:
 ,
,
где с' – скорость продольной или поперечной преломленных волн.
Наиболее распространенный способ возбуждения поперечных волн в изделии – с помощью преобразователя с призмой, угол которой лежит между первым и вторым критическими углами.
Для границы органическое стекло (плексиглас) – сталь первый критический угол падения продольной волны в плексигласе равен 27,5°. При этом угол преломления для продольной волны равен 90°, а для поперечной волны b = b' будет 33°. Второй критический угол - b = b'' = 57,5°.
Когда распространяющаяся в твердом теле волна падает на его поверхность, то возникает также две отраженные волны. При падении на поверхность поперечной волны существует третий критический угол. При нем продольная отраженная волна сливается с поверхностью и отражается одна поперечная волна. Для стали этот угол j' = 33°.
Колебание частиц в поперечных волнах, возникающих в результате трансформации из продольной волны, происходит в той же плоскости, что и в продольной волне – в плоскости падения (см. рис. 2.11.). Такую поперечную волну называют волной с вертикальной поляризацией (также SV или TV-волной). В поперечной волне с горизонтальной поляризацией (SH или ТН-волне) частицы колеблются в направлении, перпендикулярном плоскости. Такие волны можно возбудить только преобразователями специального типа.
При нормальном (т.е. перпендикулярном к границе) падении (рис. 2.11,а) коэффициенты отражения R и прозрачности D для амплитуд колебаний равны:
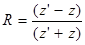 ;
; 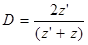 ,
,
где z и z' – волновые сопротивления первой и второй сред.
В УЗ контроле мы передаем волны из призмы в изделие, а после из изделия они попадают опять в призму. В результате волна переходит границу призма – изделие дважды: в прямом и обратном направлениях. Коэффициент прозрачности в обратном направлении:
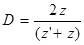 ,
,
а произведение коэффициентов прозрачности в прямом и обратном направлениях равно коэффициенту прозрачности по энергии Ď:
Ď 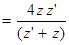 .
.
Именно этот коэффициент прозрачности важен для УЗ контроля.
Величины коэффициентов отражения и прозрачности при наклонном падении иные, чем при нормальном (рис.2.12).
Отметим, что при первом критическом угле возбуждается головная волна, а при угле несколько большем второго критического (рис. 2.11, е) возникает поверхностная рэлеевская волна. Для границы оргстекло – сталь угол падения, при котором возбуждается волна Рэлея - 65°.
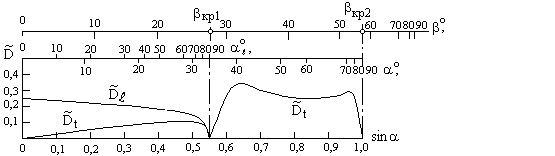 |
Рис. 2.12. Кривые изменения коэффициента прохождения продольной Ďl и поперечной Ďt волн в зависимости от угла падения b на границе оргстекло-сталь.
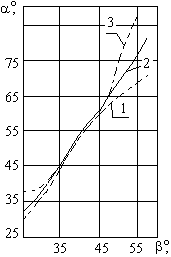 Следует отметить, что в определенном диапазоне углов теоретические значения коэффициентов прохождения отличаются от экспериментальных. Это приводит к несоответствию закону Снеллиуса. Например, при b=30° al=37°, aэ=39°; при b=53° al=76°, aэ=72°, где al– угол ввода, рассчитанный по закону Снеллиуса; aэ - экспериментальный угол ввода. Указанное обстоятельство объясняется тем, что закон Снеллиуса и полученные выражения для расчета коэффициентов отражения и прохождения справедливы в случае плоской волны. У реальных преобразователей, как правило, пучок расходящийся, и у каждого из лучей пучка свой коэффициент прохождения. Установлено также, что центральный луч отклоняется от направления акустической оси, рассчитанного по закону Снеллиуса, в зависимости от произведения радиуса а пьезоэлемента на частоту f. Отклонения тем меньше, чем больше это произведение (рис. 2.13).
Следует отметить, что в определенном диапазоне углов теоретические значения коэффициентов прохождения отличаются от экспериментальных. Это приводит к несоответствию закону Снеллиуса. Например, при b=30° al=37°, aэ=39°; при b=53° al=76°, aэ=72°, где al– угол ввода, рассчитанный по закону Снеллиуса; aэ - экспериментальный угол ввода. Указанное обстоятельство объясняется тем, что закон Снеллиуса и полученные выражения для расчета коэффициентов отражения и прохождения справедливы в случае плоской волны. У реальных преобразователей, как правило, пучок расходящийся, и у каждого из лучей пучка свой коэффициент прохождения. Установлено также, что центральный луч отклоняется от направления акустической оси, рассчитанного по закону Снеллиуса, в зависимости от произведения радиуса а пьезоэлемента на частоту f. Отклонения тем меньше, чем больше это произведение (рис. 2.13).
Рис. 2.13. Зависимость a от b, характеризующая отклонение центрального луча (1,2), соответствующего максимуму сигнала, от акустической оси (3) для ПЭП с плексигласовой призмой, излучающего в сталь: 1 – af=5мм×МГц: 2 – af=15мм×МГц.
Вблизи третьего критического угла j' (несколько больше него) происходит явление незеркального отражения – смещения пучка отраженных лучей вдоль поверхности (рис. 2.14,а) вследствие переноса энергии продольной волной, слившейся с поверхностью. Точка отражения центрального луча не совпадает с точкой падения. В результате лучи, которые не должны были бы отразиться от дефекта D (рис. 2.14,б) по законам геометрического отражения, в действительности могут отразиться от него.
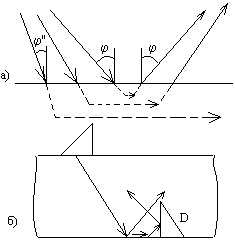
Рис. 2.14. Незеркальное отражение (а) и его влияние на отражение от дефекта (б).
Прохождение через слой.
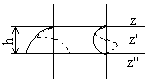 Очень тонкий промежуточный слой слабо влияет на коэффициенты отражения и прозрачности. С увеличением толщины слоя h амплитуды прошедших и отраженных волн имеют максимумы и минимумы. Если волновое сопротивление слоя z' меньше (или больше), чем обоих сред z и z'' (рис.2.15), то коэффициент отражения R больше или равен R в отсутствие слоя. Однако прохождение улучшается, если z' лежит в интервале между z и z''. Максимальная прозрачность, т.е. D=1 (просветление) достигается при условиях:
Очень тонкий промежуточный слой слабо влияет на коэффициенты отражения и прозрачности. С увеличением толщины слоя h амплитуды прошедших и отраженных волн имеют максимумы и минимумы. Если волновое сопротивление слоя z' меньше (или больше), чем обоих сред z и z'' (рис.2.15), то коэффициент отражения R больше или равен R в отсутствие слоя. Однако прохождение улучшается, если z' лежит в интервале между z и z''. Максимальная прозрачность, т.е. D=1 (просветление) достигается при условиях:
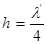 ; z' = z z'',
; z' = z z'',
где l' – длина волны в слое. Рис.2.15.
Дата добавления: 2015-08-14; просмотров: 15472;
