Упругие среды.

В твердых, жидких и газообразных средах существует упругость объема, а в твердом теле также упругость формы, то есть твердое тело стремится сохранить свою форму. Это свойство твердого тела связано со сдвиговой упругостью. Например, два слоя жидкости можно легко сдвинуть друг относительно друга, а две плоскости в твердом теле будут сопротивляться сдвигу. Попытка их сдвинуть приведет к возникновению сдвиговых колебаний.

Таким образом, во всех средах существуют колебания растяжения-сжатия. Волны с такими колебаниями – это объемные продольные волны или волны растяжения – сжатия. Колебания частиц в них происходят вдоль направления распространения волны (рис. 2.4а).

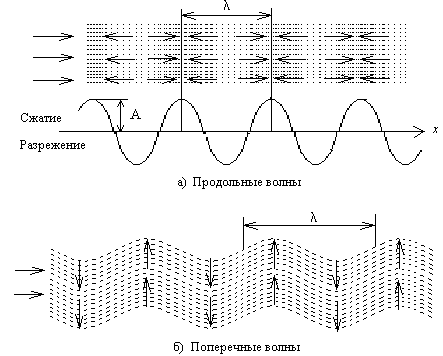В твердом теле существуют также объемные волны сдвига. Колебания частиц в них происходят поперек направления распространения волны, их поэтому называют поперечными волнами (рис. 2.4б). Скорость распространения поперечной волны приблизительно в два раза (точнее в 1,8-1,9 раза) меньше, чем продольных. Таким образом С_t=0,55 С_l.

Например, в стали скорость продольной волны – 5,90 мм/мкс, а поперечной – 3,23 мм/мкс. Скорость волны (продольной) в жидкости значительно меньше, например, в воде при комнатной температуре – 1,49 мм/мкс.

Часто встречается понятие фазы колебаний. Она характеризует состояние колебательного процесса в определенный момент времени. Если колебания непрерывные, то фаза колебаний повторяется через каждый период. Говорят, что два колебания находятся в противофазе, если их фазы отличаются на полпериода. В этом случае колеблющиеся точки будут отклоняться от среднего положения на одинаковые расстояния, но в разные стороны. В волне точки находятся в противофазе, если расстояние между ними равно l/2. Для импульсов строгая повторяемость фаз отсутствует.

В математике строго доказано, что любой импульс можно представить как сумму непрерывных (гармонических) колебаний разной частоты, имеющие разные амплитуды и начальные фазы. Набор таких гармонических колебаний называют спектром импульса. Он зависит от формы и длительности импульса. Чем короче импульс, тем в его спектре больше разных частот (спектр шире) за счет увеличения амплитуд высокочастотных (по сравнению с основной частотой) составляющих.

В твердом теле кроме продольных и поперечных существуют также специфические волны вдоль поверхности – поверхностные волны. Это волны Рэлея; скорость их немного меньше поперечных волн (для стали – 3 мм/мкс) и волны, которые в нашей стране называют головными, а за рубежом – ползучими (скорость как у продольных). С_s=0,93С_t; S_r=1,03 C_l.

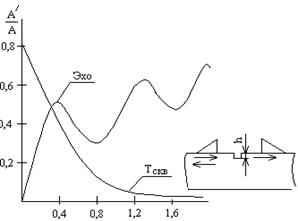Амплитуда рэлеевской поверхности волны имеет максимум на поверхности и уменьшается в 10 раз на глубине около l_s – длины поверхностной волны. Это видно на кривой ослабления сквозного сигнала (рис. 2.5). Осцилляции отраженного сигнала объясняются интерференцией импульсов, отраженных от грани и кончика риски. Рэлеевская волна распространяется на большие расстояния, следуя изгибам поверхности. На выпуклой поверхности скорость ее увеличивается, а на вогнутой – уменьшается, но одновременно растет затухание.

Головную волну можно представить как идущий от излучателя пучок лучей продольных волн. Максимальную амплитуду имеет луч под углом скольжения (угол к поверхности) 12 … 15°. Амплитуда луча, идущего вдоль поверхности, очень мала и быстро убывает с расстоянием вследствие порождения поперечной волны, распространяющейся под углом, равным третьему критическому (33° для стали). Достигая нижней поверхности, она порождает там головную волну, которую также используют для контроля.

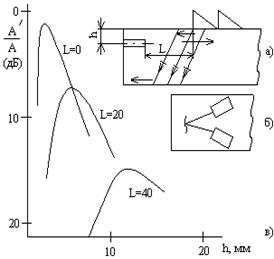В соответствии с этим изменяется чувствительность к дефектам (рис. 2.6,в). Головная волна практически не чувствительна к поверхностным дефектам (на глубине 0,5 мм и менее) и имеет максимум чувствительности на глубине 4 …10 мм, в зависимости от расстояния от преобразователя (длина = 10 … 50 мм). Использованы излучатель и приемник, расположенные один за другим (схема тандем, рис. 2.6, а). Схема с преобразователями, расположенными рядом (дуэт, рис. 2.6, б), обеспечивает лучшую чувствительность в узкой области вблизи точки пересечения центральных лучей излучателя и приемника.

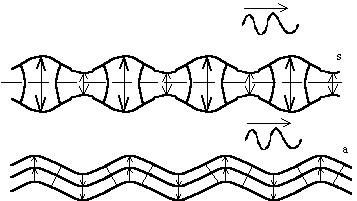
В результате волнового эффекта в пластинах и стержнях возникают нормальные волны: волны в пластинах (волны Лэмба) (рис. 2.7) и стержневые (волны Порхгаммера). Колебания охватывают все сечения пластины или стержня. Разные моды этих волн отличаются распределением колебаний по толщине (рис. 2.7). В модах выше нулевой имеются узловые поверхности, где напряжения равны нулю и совпадающие с ними дефекты выявляются плохо.

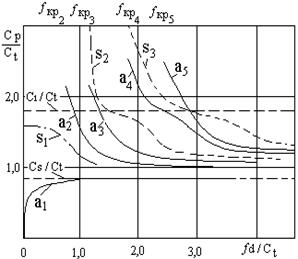
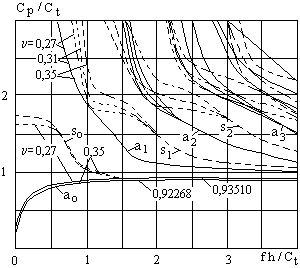
Скорости продольных, поперечных и поверхностных волн не зависят от частоты. Скорости волн в пластинах и стержнях зависят от произведения толщины изделия h на частоту f, деленное на скорость поперечной волны с_r. Это явление называют дисперсией скорости. На рис. 2.8 и 2.9 приведены дисперсионные кривые для их фазовых скоростей. Сплошные кривые для антисимметричных (а) мод, а штриховые – для симметричных (s). Примеры таких мод показаны на рис. 2.6. Нулевые моды переходят при увеличении толщины в поверхностную волну, остальные – в поперечную. Фазовые скорости позволяют рассчитать длину волны 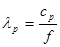и определить условия возбуждения волны. Вдоль пластины (стержня) импульс распространяется с групповой скоростью с_g, которая связана с с_р формулой:

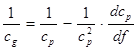
При 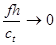для моды и с_g = с_р.

Рис. 2.7. Деформация пластины при распространении

симметричных и антисимметричных волн.