Скорость звука.
Скорость звука – скорость перемещения в среде упругой волны при условии, что форма ее профиля остается неизменной. Напр., для плоской волны, бегущей без изменения формы со скоростью с в направлении оси x, звуковое давление можно записать в виде: р=р(х-сt), где t – время, а функция р дает форму профиля волны. Для гармонич. волны р= А cos(w t – kx + j). Звуковая волна выражается через частоту w и волновое число k формулой 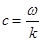 . Скорость гармоничной волн называется также фазовой скоростью звука. В средах, в которых форма волн произвольной формы меняется при распространении, гармоничные волны тем не менее сохраняют свою форму, но фазовая скорость оказывается различной для различных частот, т.е. имеет место дисперсия скорости звука. В этих случаях пользуются также понятием групповой скорости. При больших амплитудах упругой волны появляются нелинейные эффекты, приводящие к изменению формы любых волн, в т.ч. гармонических, так что понятие скорости звука теряет определенность. В этом случае скорость распространения каждой точки профиля волны зависит от амплитуды давления в этой точки. Эта скорость растет с ростом давления в данной точке профиля, что приводит к искажению формы волны.
. Скорость гармоничной волн называется также фазовой скоростью звука. В средах, в которых форма волн произвольной формы меняется при распространении, гармоничные волны тем не менее сохраняют свою форму, но фазовая скорость оказывается различной для различных частот, т.е. имеет место дисперсия скорости звука. В этих случаях пользуются также понятием групповой скорости. При больших амплитудах упругой волны появляются нелинейные эффекты, приводящие к изменению формы любых волн, в т.ч. гармонических, так что понятие скорости звука теряет определенность. В этом случае скорость распространения каждой точки профиля волны зависит от амплитуды давления в этой точки. Эта скорость растет с ростом давления в данной точке профиля, что приводит к искажению формы волны.
Скорость звука в газах и жидкостях. В газах и жидкостях звук распространяется в виде объемных волн разрежения – сжатия, причем процесс происходит обычно адиабатически, т.е. изменение температуры в звуковой волне не успевает выравниваться, т.к. за ½ периода тепло из нагретых (сжатых) участков не успевает перейти к холодным (разреженным).
Скорость звука в газах меньше, чем в жидкостях, а в жидкостях, как правило, меньше, чем в твердых телах. В таблице 2.1 приведены значения скорости звука для некоторых газов и жидкостей.
Таблица 2.1
| Скорость звука в газах при 0° | Скорость звука в жидкостях при 20°С | ||
| Газ | с, м/с | Жидкость | с, м/с |
| Азот | Вода | ||
| Кислород | Ацетон | ||
| Воздух | Бензол | ||
| Гелий | Толуол | ||
| Водород | Спирт этиловый | ||
| Неон | Четыреххлористый углерод | ||
| Метан | Ртуть | ||
| Аммиак | Глицерин | ||
| Углекислый газ | |||
| Иодистый водород |
Скорость звука в идеальных газах при заданной температуре не зависит от давления и растет с ростом температуры как 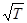 , где Т – абсолютная температура. Изменение скорости звука, отнесенное к одному градусу, равно
, где Т – абсолютная температура. Изменение скорости звука, отнесенное к одному градусу, равно 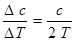 . При комнатной температуре относительное изменение скорости звука в воздухе при изменении температуры на 1 градус составляет примерно 0,17%. В жидкостях скорость звука, как правило, уменьшается с ростом температуры, и изменение температуры на один градус составляет, напр., - 5,5 м/с×град для ацетона и – 3,6 м/с×град для этилового спирта. Исключением из этого правила является вода, в которой скорость звука при комнатной температуре увеличивается с ростом температуры на 2,5 м/с×град, достигает максимума при температуре » 74°С и с дальнейшим ростом температуры уменьшается. Скорость звука в воде растет с увеличением давления примерно на 0,01% на 1 атмосферу; кроме того, скорость звука в воде растет с увеличением содержания растворенных в ней солей.
. При комнатной температуре относительное изменение скорости звука в воздухе при изменении температуры на 1 градус составляет примерно 0,17%. В жидкостях скорость звука, как правило, уменьшается с ростом температуры, и изменение температуры на один градус составляет, напр., - 5,5 м/с×град для ацетона и – 3,6 м/с×град для этилового спирта. Исключением из этого правила является вода, в которой скорость звука при комнатной температуре увеличивается с ростом температуры на 2,5 м/с×град, достигает максимума при температуре » 74°С и с дальнейшим ростом температуры уменьшается. Скорость звука в воде растет с увеличением давления примерно на 0,01% на 1 атмосферу; кроме того, скорость звука в воде растет с увеличением содержания растворенных в ней солей.
В сжиженных газах скорость звука больше, чем в газе при той же температуре. Так, например, в газообразном азоте при температуре минус 195°С скорость звука равна 176 м/с, а в жидком при той же температуре минус 859 м/с; в газообразном и жидком гелии при минус 269°С она равна соответственно 102 м/с и 198 м/с.
В водных растворах солей скорость звука растет с ростом концентрации по всем интервале концентраций. Таким образом, измерения скорости звука могут служить для определения и контроля концентрации компонент смесей и растворов.
Скорость звука в твердых телах. Скорость звука в изотропных твердых телах определяется модулями упругости вещества. В неограниченной твердой среде распространяются продольные и сдвиговые (поперечные) упругие волны, причем фазовая скорость звука для продольной волны равна:
 , а для сдвиговой
, а для сдвиговой
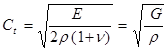 ,
,
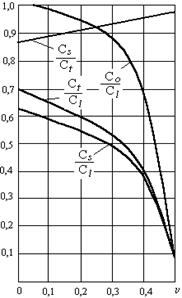
где Е – модуль Юнга; r - плотность вещества; G – модуль сдвига; n - коэффициент Пуассона; К – модуль объемного сжатия. В металлах, где n=0,3, можно проследить зависимость отношения скоростей звука по рис. 2.2.
Рис. 2.2. Зависимость соотношения скоростей продольных 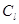 , поперечных
, поперечных 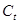 , поверхностных
, поверхностных 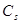 волн и волн в стержнях
волн и волн в стержнях 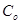 (при d<<1) от коэффициента Пуассона.
(при d<<1) от коэффициента Пуассона.
Скорость распространения продольных волн всегда больше, чем скорость сдвиговых волн, а именно выполняется соотношение 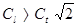 . Значения продольной и поперечной скорости звука для некоторых твердых тел приведены в таблице 2.2.
. Значения продольной и поперечной скорости звука для некоторых твердых тел приведены в таблице 2.2.
Таблица 2.2
Скорость звука в некоторых твердых веществах.
| Материал | 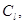 м/с м/с
| 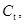 м/с м/с
| Сст, м/с |
| Бетон | 4200-5300 | - | - |
| Полистирол | 2350-2380 | 1860-2240 | |
| Железо | 5835-5950 | 3180-3240 | 5000-5200 |
| Золото | 3200-3240 | ||
| Платина | 3260-3960 | 1670-1730 | 2690-2800 |
| Свинец | 1960-2400 | 700-790 | 1200-1320 |
| Цинк | 4170-4210 | 3700-3850 | |
| Серебро | 3650-3700 | 1600-1690 | 2610-2800 |
| Углеродистые стали | 5900 - 5940 | 3220 – 3250 | 5099-5177 |
| Нержавеющие стали | 5660 – 6140 | 3120 – 3250 | |
| Титан | |||
| Медь | |||
| Алюминиевый сплав АМГ |
В ограниченных твердых телах, кроме продольной и поперечной волн, имеются и другие типы волн. Так, вдоль свободной поверхности твердого тела или вдоль границы его с другой средой распространяется специфический вид волн – поверхностные волны, скорость которых меньше, чем все остальные скорости звука для данного твердого тела. В пластинах, стержнях и других твердых акустических волноводах распространяются нормальные волны, скорость которых определяется не только упругими характеристиками вещества, но и геометрией тела. Так, например, скорость звука для продольной волны в стержне, поперечные размеры которого много меньше длины волны, равна: 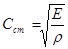 . В таблице 2.2 приведены значения скорости звука в тонком стержне для некоторых материалов.
. В таблице 2.2 приведены значения скорости звука в тонком стержне для некоторых материалов.
В металлах и сплавах скорость звука существенно зависит от обработки, которой был подвергнут металл: прокат, ковка, отжиг и т.п. Частично это явление связано с дислокациями, наличие которых также влияет на скорость звука (в табл. 2.2 даны наибольшие и наименьшие значения по данным литературы). В металлах, как правило, скорость звука уменьшается с ростом температуры.
Дата добавления: 2015-08-14; просмотров: 3748;
