Учет пространственной работы температурного блока при работе мостовых кранов

Лекция №2(18)

Учет пространственной работы температурного блока при работе мостовых кранов

Покрытие здания из железобетонных плит, соединенных сваркой закладных деталей с замоноличиванием швов, представляет собой жесткую в своей плоскости горизонтальную связевую диафрагму. Колонны здания, объединенные горизонтальной связевой диафрагмой в поперечные и продольные рамы, работают как единый пространственный блок. Размеры такого блока в плане определяются расстояниями между температурными швами (рис.1, а).

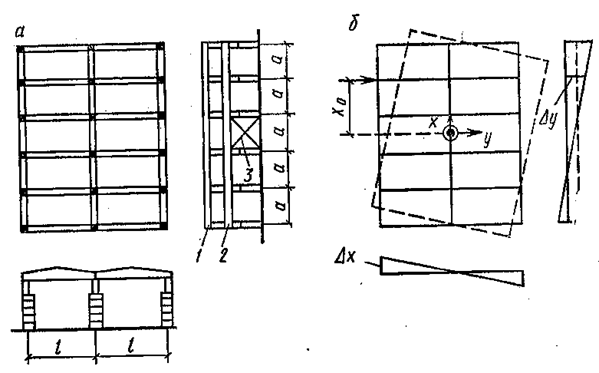
Рис.1. Пространственный блок одноэтажного каркасного здания:

а - схема блока; б - схема перемещения блока; 1 - покрытие; 2 - подкрановая балка; 3 - вертикальные связи по колоннам

Нагрузки от массы покрытия, снега, ветра приложены одновременно ко всем рамам блока, при этих нагрузках пространственный характер работы каркаса здания не проявляется и каждую плоскую раму можно рассчитывать в отдельности. Нагрузки же от мостовых кранов приложены к двум-трем рамам блока, но благодаря горизонтальной связевой диафрагме в работу включаются и остальные рамы блока; происходит пространственная работа.

В каркасном здании из типовых элементов с регулярным шагом колонн и постоянной жесткостью сечений колонн центр жесткости блока (т. е. точка приложения равнодействующей реактивных сил при поступательном перемещении блока) совпадает с его геометрическим центром. Если поместить начало координат в этом центре и принять что х - координата поперечной рамы, а у продольной рамы (рис,1, б), то, приложив к поперечной раме с координатой хо силу F, можно определить перемещение этой рамы. Перемещение блока от силы F - поступательное, а от момента 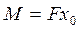- вращательное. Если 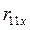- реакция поперечной рамы от единичного перемещения Δ= 1, то поступательное перемещение блока

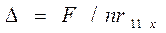, (1)

где n - число поперечных рам блока.

При вращательном перемещении жесткой в своей плоскости горизонтальной связевой диафрагмы на угол φ = 1 поперечные рамы получают перемещение равное х·tgφ, но поскольку конечный угол φ будет малым и, следовательно, tgφ=φ=1, поперечные рамы получают перемещение, равное их координате х, а продольные рамы - равное у. При этом возникают реакции:

в поперечных рамах

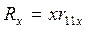; (2)

в продольных рамах

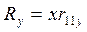, (3)

где 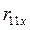- реакция продольной рамы от смещения Δ=1 (определяется с учетом сопротивления вертикальных связей по колоннам).

Кручением колонн при вращении горизонтальной диафрагмы ввиду его малости можно пренебречь.

Угловая жесткость блока или реактивный момент блока от единичного угла поворота диафрагмы φ = 1

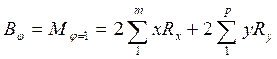, (4)

где( m= n/2, когда n - число поперечных рам четное, или m=(n-l) /2, когда n - число нечетное; р = q /2, когда q - число продольных рам - четное, или р=(q-l)/2, когда q - число нечетное,

Угловая жесткость блока с учетом значения реакций согласно формулам (2), (3), составляет

, (5)

где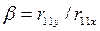

Угол поворота блока вокруг центра вращения

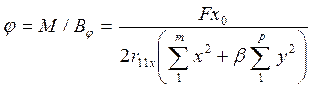. (6)

Перемещение поперечной рамы с координатой 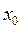от силы F находят суммированием перемещений - поступательного и от вращения блока. Тогда

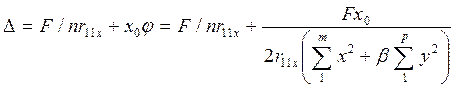(7)

Находит реактивную силу от единичного перемещения Δ= 1 поперечной рамы, приравняв единице перемещение по формуле (7). Тогда

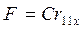, (8)

где

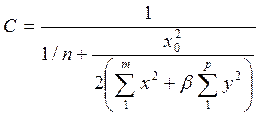. (9)

Коэффициент C характеризует пространственную работу каркаса, состоящего из поперечных и продольных рам. Следует принять во внимание податливость соединений плит покрытия, которую на основании исследований оценивают коэффициентом 0,7 к значению C, а также учесть загружение нагрузкой от мостовых кранов рам, смежных с рассчитываемой, коэффициентом 0,7. Тогда

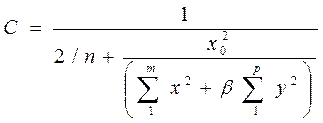. (10)

Если учитывать пространственную работу рам лишь одного поперечного направления, то в упрощенном решении при β=0 из формулы (9)

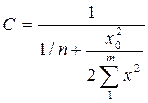. (11)

Тогда при длине блока 72 м для второй от торца блока поперечной рамы, находящейся в наименее благоприятных условиях (в части помощи, оказываемой работой соседних рам), при шаге 12 м C=3,5; при шаге 6 м C=4,7.

Рис.2. К пространственному расчету одноэтажного каркасного здания