Особенности определения усилий в двухветвевых и ступенчатых колоннах

При двухветвевых колоннах расчет поперечной рамы с учетом пространственной работы каркаса здания аналогичен расчету рамы со сплошными колоннами.

Двухветвевая колонна представляет собой многоэтажную однопролетную раму (рамный стержень) с расстоянием с между осями ветвей, расстоянием s между осями распорок, числом сплошной части, общей длиной l (рис.3, а). Поскольку ригелями рамного стержня служат короткие жесткие распорки, а стойками - менее жесткие ветви колонны, деформациями ригелей можно пренебречь и с практически достаточной точностью считать их абсолютно жесткими. Другая возможная расчетная схема - с упругими ригелями - как показали исследования, приводит к несущественному уточнению результатов расчета. Для определения реакций при неподвижной верхней опоре двухветвевую колонну рассматривают как стержень, обладающий, изгибной жесткостью 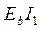и конечной сдвиговой жесткостью К. Сдвиговая жесткость двухветвевой колонны обусловлена местным изгибом ветвей, она равна силе, вызывающей перекос ветвей на единичный угол (рис.3, б):

. (12)

где I - момент инерции ветви.

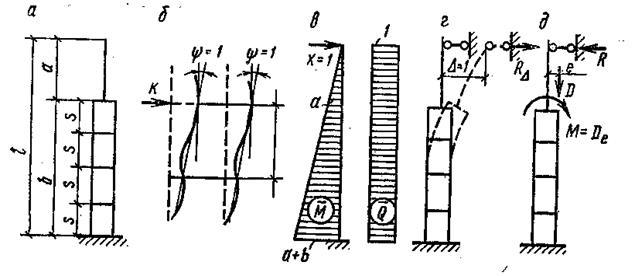
Рис.3. К расчету двухветвевой колонны:

а - расчетная схема; б - местный изгиб ветвей; в - эпюpa моментов от единичной силы; г – деформация от единичного смещения; д - реакция верхнего конца колонны от кранового момента

Если приложить к верхнему концу рассматриваемого стержня (пока без верхней опоры) силу Х = 1 (рис.3, в), то перемещение

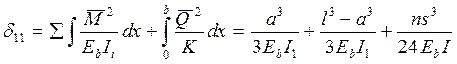, (13)

где 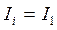-в нижней части колонны; 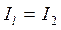верхней части.

Отсюда реакция от перемещения Δ= 1 верхнего конца колонны (рис.3, г)

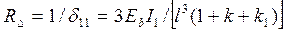. (14)

где 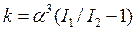; ; 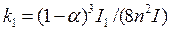(15)

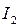- момент инерции верхней части колонны; А – площадь сечения ветви; 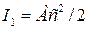- момент инерции нижней части колонны (значением 2l пренебрегают как относительно малым); .

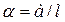Если двухветвевая колонна загружена крановым моментом М, то перемещение

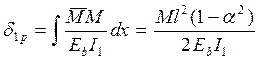. (16)

Реакция R при неподвижной верхней опоре двухветвевой колонны (рис.3,д)

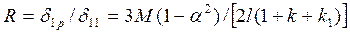. (17)

Здесь знак минус опущен.

Формулы реакций R универсальны, так как могут применяться не только для двухветвевых колонн, но и для ступенчатых при k=0, колонн постоянного сечения при 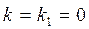. По этим же формулам в необходимых случаях можно найти перемещения 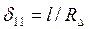; 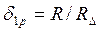,а также выполнить расчет рамы с учетом упругой заделки колонны в фундаменте.

При расчете рамы на изменение температуры Δt учет действительной податливой заделки колонны в фундаменте (а также учет действительной жесткости колонны на участках с трещинами) приводит к уменьшению изгибающего момента. Реакция от поворота колонны в нижнем сечении на угол φ = 1 составляет

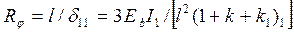. (18)

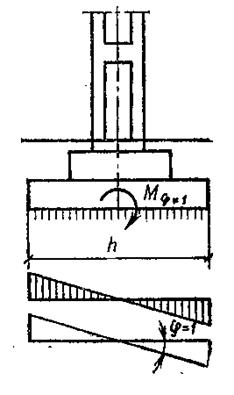
Рис.4. К расчету податливости заделки колонн

Реактивный момент от поворота фундамента на угол φ= 1 (рис.4) находят следующим образом. Осадка края фундамента с размерами сторон в плане b×h составляет y=0,5h tgφ =0,5h (деформациями самого фундамента пренебрегают). краевое давление фундамента на основание

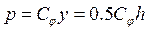, (19)

где 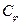- коэффициент постели при неравномерном обжатии основания.

Реактивный момент от поворота фундамента

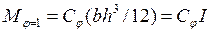, (20)

где 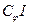- угловая жесткость фундамента.

После определения из расчета поперечной рамы упругих реакций Re вычисляют усилия в расчетных сечениях М, N, Q относительно геометрической оси двухветвевой колонны. Усилия же в ветвях и распорках определяют в последующем расчете при подборе сечений.

Продольные силы в ветвях колонны

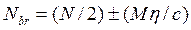, (21)

где М, N - расчетные усилия по оси двухветвевой колонны; 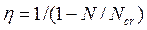-коэффициент продольного изгиба.

При определении коэффициента 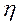следует учесть влияние гибкости ветвей в плоскости изгиба двухветвевой колонны как для составного сечения (рис. 5, а).

Приведенный радиус инерции 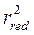зависит от радиуса инерции сечения нижней части колонны 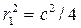и от радиуса инерции сечения ветви .

Приведенная гибкость должна удовлетворять зависимости

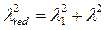, (22)

или, при ,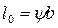

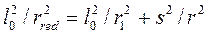. (23)

После подстановки значений и 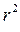сокращения на 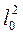получим

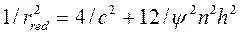, (24)

отсюда

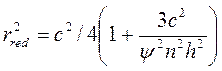, (25)

здесь n=b/s - число панелей двухветвевой колонны.

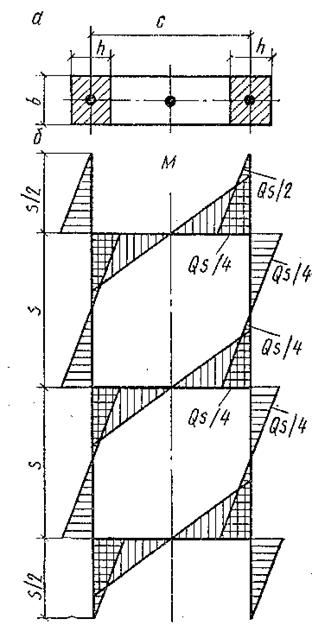
Рис.5. К определению усилий в ветвях и распорах колонны:

а - сечение колонны; б - эпюра моментов

Условная критическая сила

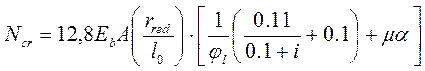, (26)

где А, μ - соответственно площадь сечения и коэффициент армирования ветви. определении

При определении коэффициента

, (27)

где моменты М и вычисляют относительно оси, проходящей через ось ветви.

Изгибающий момент ветви при нулевой точки моментов в середине высоты панели (рис.5)

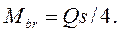(28)

Изгибающий момент и поперечная сила в распорке равны:

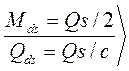. (29)

Если одна из ветвей при определении продольной силы по формуле (21) окажется растянутой, то следует выполнить расчет двухветвевой колонны с учетом пониженной жесткости этой растянутой ветви. В этом случае изгибающие моменты в сжатой ветви и распорках определяют из условия передачи всей поперечной силы в сечении колонны на сжатую ветвь.