Экспериментальные установки, использующиеся для проведения кинетических исследований. Идеальные реактора
После первого этапа кинетического исследования, литературного поиска данных о механизме и кинетике изучаемой реакции переходят к этапу выбора вариантов проведения процесса. На этом этапе необходимо выбрать установку для экспериментального исследования. Так как нам нужна зависимость скорости реакции от параметров
r = f(P, T, C)
выбирают идеальные установки, для которых уравнения являются простыми, так называемые модельные реактора.
1. ИПР (РПД) – идеальный периодический реактор (реактор периодического действия);
2. РИВ – реактор идеального вытеснения;
3. РПС – реактор полного смешения или РИС.
РПД – это реактор, действие которого заключается в загрузке всех реагентов, проведении реакции в режиме интенсивного перемешивания, то есть в отсутствии диффузионного торможения.
.
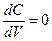В реакторе поддерживается изотермический режим:
.
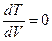A + B → C + D
Концентрация изменяется во времени.
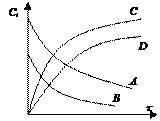
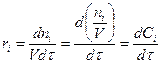
В гетерогенной среде:
.
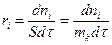Характеристическое уравнение – уравнение зависимости времени реакции от C, n, F, XA, XiA.
;
;
.
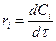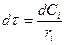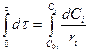Характеристическое уравнение для РПД:
.
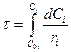Поскольку V = const:
.
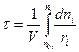Для гетерогенных:
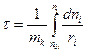
РИВ – реакционная масса движется вдоль оси, вытесняя предыдущие слои с одинаковой линейной скоростью, при этом отсутствует диффузионное торможение смеси стенками реактора. Концентрация вещества изменяется по длине реактора. Состав реакционной смеси постоянен во времени.
Здесь оперируют мольными потоками.
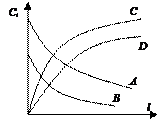
Условие идеальности:
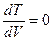изотермический реактор
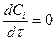стационарный режим
Для расчета характеристического уравнения используем следующие формулы:
;
;
;
.
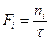
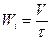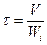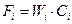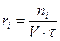В РИВ изменяется ni и V, тогда уравнение для скорости:
· для гомогенных систем:
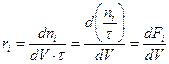
· для гетерогенных систем:
.
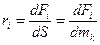Преобразуем уравнение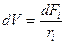 
.
Проинтегрируем:
.
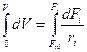Для гомогенных:
.
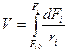Для гетерогенных:
.
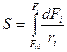
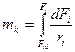Первый случай: Wi0 = const, тогда:
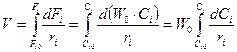
Истинное время пребывания:
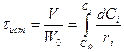
Характеристическое уравнение РИВ при условии W0 = const:
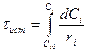
Характеристические уравнения для РПД и РИВ одинаковы!
Второй случай: Wi0 ≠ const, тогда:
;
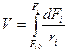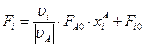
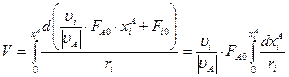
Условное время:
.
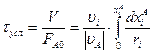Объемная скорость:
; 
.
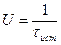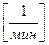Уравнения применяются для:
· однослойных, многослойных и трубчатых реакторов с фильтрующими слоями катализатора;
· реакторов с движущимся катализатором и с потоком взвеси катализатора;
· реакторов с заторможенным кипящим слоем катализатора.
Для жидкофазных реакций применяются насади. В этом случае уравнение имеет вид:
.
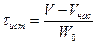Чтобы установить в реакторе стационарный режим, необходимо пропустить через реактор 3-5 объемов смеси заданного состава.
РПС – реактор представляет собой модель, объединяющая РИВ и РПД. Это проточный реактор непрерывного действия, диффузионное торможение отсутствует за счет интенсивного перемешивания.
Ci0 моментально изменяется до Ci и одинаково во всем объеме.
Условие стационарности:
.
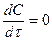Перемешивание:
.
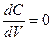Изотермичность:
.
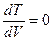Так как здесь идет и условие стационарности V = const, τ = const, то:
.
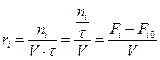Это уравнение неинтегральное и безградиентное.
Первый случай: W0 = const:
;
.
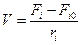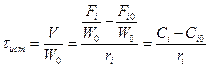Второй случай: W0 ≠ const:
.
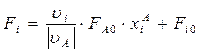
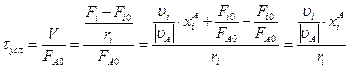Для этого реактора характерно турбинное течение потока реагента. Оно наблюдается, когда скорость циркуляционных движений газа или жидкости по высоте и сечению намного больше скорости линейного движения по оси.
В реакторе поддерживается изотермический режим. Кипящий слой катализатора не должен быть заторможен какими-либо насадками катализатора, а высота слоя должна быть небольшой. Скорость потока газа в 2…4 раза должна превышать критическую скорость начала взвешивания.
Дата добавления: 2015-08-14; просмотров: 1825;