Частотный коэффициент передачи.

При математическом исследовании систем, особый интерес представляют такие входные сигналы, которые будучи преобразованными системой остаются неизменными по форме.

Если имеется равенство:

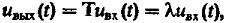(16) то Uвх (t) – является собственной функцией системы оператора T, а число 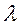- в общем случае комплексное, - его собственным значением.

Покажем, что 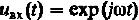при любом 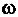есть собственная функция линейного стационарного оператора.

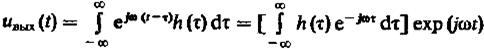(17)

Отсюда видно, что собственным значением системного оператора является комплексное число:

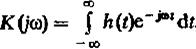(18) называется – частотным коэффициентом передачи системы .

Частотный коэффициент передачи и импульсная характеристика линейной стационарной системы связаны между собой преобразованием Фурье, т.е.

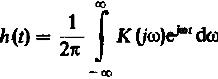(19)

Т.е. любую систему можно рассматривать во временной области с помощью импульсов или переходной характеристики, либо в частотной задавая частотный коэффициент передачи.

Амплитудно – частотная и фазочастотная характеристика.

Можно записать:

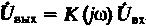(20)

Или

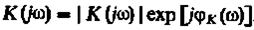(21)

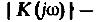Амплитудно – частотная характеристика

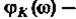фазочастотная характеристика

(ФЧХ) – системы.

Критерий Пэли – Винера.

Частотный коэффициент физически реализуемой системы должен быть таким, чтобы существовал интеграл:

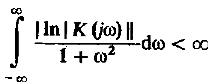(22)