Лекция 2 ВЗАИМОДЕЙСТВИЕ g-ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ

Процесс замедления g-квантов в среде нельзя считать непре­рывным, как это было сделано для тяжелых заряженных частиц, поскольку при взаимодействии с электронами и атомами среды g-квант теряет или всю свою энергию (поглощение), или значительную часть своей энергии (рассеяние). В последнем случае в результате взаимодействия g-квант существенно изменяет и направление своего движения. Поэтому достаточно одного взаимодействия, чтобы выве­сти g-квант из первоначально параллельного пучка g-квантов. В си­лу этих особенностей параллельный пучок g-квантов при прохождении через слой материала толщиной t ослабляется по экспоненциальному закону:

N = N₀exp(-md) (2.1)

где No—число g-квантов, падающих на слой толщиной d; N— число g-квантов с той же энергией и с тем же направлением после слоя материала; m — коэффициент пропорциональности, называе­мый линейным коэффициентом ослабления и имеющий размерность см^-1.

Так как характер ослабления g-излучения экспоненциальный, то имеется всегда малая, но не нулевая вероятность пройти g-кванту без соударений очень большие толщины материалов. Поэтому пробе­ги 7-квантов между соударениями могут значительно отличаться от среднего пробега.

Физический смысл коэффициента пропорциональности в формуле (2.1) следующий: пучок g-квантов ослабляется в е раз на пути 1/m, который является средним свободным пробегом g-кванта в веществе до соударения. Это легко получить, если принять во внимание, что exp (-mt) — вероятность g-кванта пройти путь t без соударения.

Тогда по определению средний путь будет равен отношению 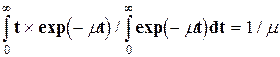.Если ввести полное сечение взаимодействия g-квантов с одним атомом s, то m = ns (n — число атомов в 1 см³ вещества).

Известно большое число различных взаимодействий электро­магнитного излучения с электронами, атомами и ядрами среды. Для регистрации g-квантов и особенно для их ослабления в среде практическое значение имеют следующие три процесса: фотоэлектри­ческое поглощение (фотоэффект), рассеяние g-квантов на свободных электронах (комптоновское рассеяние) и рождение g-квантомв поле атома пары позитрон — электрон (образование пар). Полное сечение взаимодействия g-квантов с атомами s складывается из се­чения фотоэффекта s_ф, сечения комптоновского рассеяния s_к и се­чения образования пар s_п

Для регистрации g-квантов имеет значение еще и ядерный фото­эффект (фотоядерные реакции), однако его сечение в области энергий до десятков мегаэлектронвольт незначительно в сравнении с сече­нием взаимодействия g-квантов с электронами.

При прохождении через вещество гамма-кванты взаимодействуют с электронами и ядрами, в результате их интенсивность уменьшается. В области энергий до 10 Мэв наиболее существенными процессами являются фотоэффект, эффект Комптона и образование злектрон-позитронных пар. При энергии гамма-квантов больше 10 Мэв превышается порог фотоядерных реакций и в результате взаимодействия фотонов с ядрами становятся возможны реакции типа ( ,р), ( ,n), ( ,a). Сечения фотоядерных реакций в области энергий до 100 Мэв составляют 1% полного сечения взаимодействия гамма-квантов с атомом. Однако фотоядерные реакции необходимо учитывать в процессах преобразования фотонного излучения в веществе, так как вторичные заряженные частицы, такие как протоны и альфа-частицы, могут создавать высокую плотность ионизации

Фотоэффект. Вся энергия падающего кванта hn при фотоэффекте затрачивается на вырывание электрона из атома. При фотоэффекте фотон поглощается атомом и высвобождается электрон (рис.2.1).

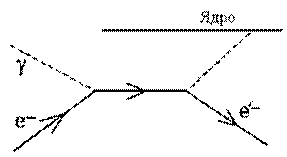
Рис. 2.1 – Схематическое изображение фотоэффекта

Энергию электрона можно определить из следующего соотношения:

E_e= hn - B_e (2.2)

где В_e — энергия связи электрона. Из приведенного соотношения ясно, что фотоэффект возможен только в тех случаях, когда hn > B_e. Поэтому сечение фотоэффекта претерпевает резкие скачки при энер­гиях, равных энергиям ионизации К-, L-... оболочек.

Расчеты сечения фотоэффекта показали, что он происходит глав­ным образом на K-оболочке (около 80%). Для энергии фотонов hn»mc², но не близких к границе K-полосы поглощения, сечение фотоэффекта на K-оболочке получено в виде

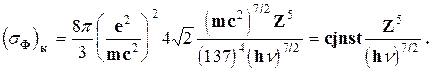(2.3)

В этом выражении Z — заряд ядра атома; (s_ф)_К — сечение фото­эффекта, см²/атом. Полное сечение фотоэффекта s_ф» 5 (s_ф)_К/4.

Как видно из (2.3), сечение фотоэффекта очень быстро умень­шается с ростом энергии квантов и с уменьшением заряда ядра. Формула (2.3) неточно описывает поведение сечения в областях, близких к границе полосы поглощения. Однако она правильно пе­редает качественную зависимость сечения фотоэффекта от энергии и заряда ядра.

При энергиях hn>>mc² сечение фотоэффекта обратно пропорцио­нально энергии g-квантов. По этой причине для тяжелых элемен­тов, таких, как свинец, фотоэффект имеет заметное значение даже при энергиях около 5 Мэв.

Фотоэффект сопровождается характеристическим излучением атомов в результате переходов электронов на вакантные места в электронной оболочке атома. Характеристическое излучение не всегда сопровождает фотоэффект. Энергию можно передать электро­нам внешней оболочки атома. В этом случае кроме фотоэлектронов с энергией Е_е появляются так называемые оже-электроны.0же-электроны с большой вероятностью наблюдаются при фотоэффекте на атомах с малыми и средними значениями Z.

Угловое распределение фотоэлектронов зависит от их энергии. При малых энергиях (десятки килоэлектронвольт) фотоэлектроны преимущественно испускаются в направлении, перпендикулярном пучку g-квантов. С ростом энергии средний угол вылета фотоэлектро­нов уменьшается (20—30° при энергиях 0,5 Мэв.)

Комптоновское рассеяние. Если энергия g-кванта значительно больше энергии связи электрона, то можно рассматривать упругое столкновение g-кванта со свободным электроном. В случае эффекта Комптона, часть энергии -кванта преобразуется в кинетическую энергию электронов отдачи, а часть энергии уносит рассеянный фотон (рис. 2.2).

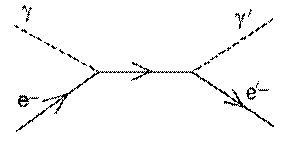
Рис. 2.2 – Схематическое изображение эффекта Комптона

Тогда из законов сохранения энергии и импульса можно получить связь между энер­гией рассеянного g-кванта. hn', энергией падающего кванта hn и углом рассеяния q (относительно первоначального направления g-кванта), а также связь между энергией комптон-электрона Е_е и его углом вылета j. Эти соотношения следующие:

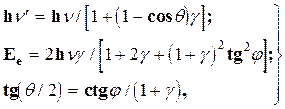(2.4)

где g = hn(mc²). Из приведенных соотношений, в частности, сле­дует, что кванты, рассеянные на углы q > 90°, всегда имеют энергию hn’£ mc²/2 независимо от начальной энергии, а при q<180° hn’£ mc²/2. Дифференциальное сечение комптоновского рассеяния, вычисленное по формуле Клейна — Нишины — Тамма, прек­расно согласуется с экспериментальными данными. Наиболее ком­пактная запись этой формулы с учетом (2.4) выглядит так:

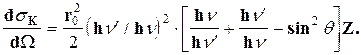(2.5)

Здесь приведена вероят­ность комптоновского рас­сеяния в направлении q в единице телесного угла на Z электронах (т.е. на атоме с зарядом Z); r₀ = е²/ (mc²) — классический радиус электро­на. При энергиях квантов очень малых (hn < mc²) энер­гии рассеянных квантов рав­ны энергиям падающих [см. (2.4)],а сечение

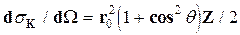(2.6)

Полное сечение комптоновско­го рассеяния мож­но получить, интегрируя (2.5) по всему телесному углу:

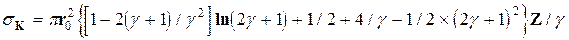(2.7)

где g=hn/(mc²).

Для некоторых практических задач важное значение имеют диф­ференциальное сечение ds_Ke/dW на единицу угла для числа электро­нов, рассеянных на угол j, и дифференциальное сечение передачи электрону энергии в интервале от Е_e до E_e+dE_e. Эти сечения мож­но получить из (2.5) при замене соответствующих переменных

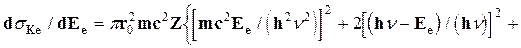
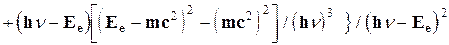(2.8)

Электроны от­дачи при комптон-эффекте направлены в основном вдоль первона­чального направления движения g-квантов. Чем выше энергия ".'-квантов, тем анизотропия больше. Если энергия g-квантов пре­вышает 2 Мэв, то большинство электронов имеют углы вылета меньше 20°.

В некоторых случаях необходимо учитывать скорости электро­нов, взаимодействующих с g-квантами. Оказывается, что движение электронов в атомах приводит к заметному разбросу электронов отдачи по энергиям. В частности, если импульс фотона меньше импуль­са летящего навстречу ему электрона, то фотон не теряет, а приоб­ретает энергию. Рассмотрим это. Пусть импульс электрона мал в сравнении с импульсом g-кванта. Оценим, насколько изменится энергия электрона отдачи при лобовом соударении с фотоном в за­висимости от направления импульса электрона. Закон сохранения энергии имеет вид

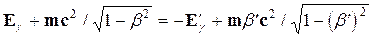(2.9)

где Е_g и Е’_g — энергия g-кванта до и после столкновения с электро­ном; b и b' — скорости электрона в долях скорости света до и после столкновения. Закон сохранения импульса

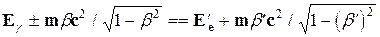(2.10)

Сложим эти уравнения и после небольших преобразований, ис­пользовав

;

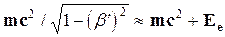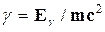, (2.11)

в случае малых энергий электронов до соударения, таких, что 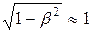, получим для кинетической энергии электрона после соударения следующее выражение:

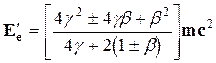(2.12)

Здесь b в скобках берется с минусом при движении электрона навст­речу g-кванту, а с плюсом — при движении электрона по направле­нию движения g-кванта. Если считать, что b² << 1, то легко получить:

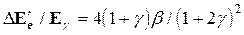(2.13)

Из этого соотношения, в частности, следует что даже для сравни­тельно медленных электронов (например, при b=0,02) неопределен­ность в энергии электронов отдачи может достигать нескольких про­центов. Аналогично легко вычислить энергию фотона при лобовом соударении с электроном, имеющим значительно больший импульс, чем фотон.

Образование пар. Гамма-квант в электрическом поле электрона или ядра может образовать пару электрон — позитрон. Такой про­цесс превращения g-кванта в две частицы - процесс эндотермичес­кий и может происходить в том случае, если энергия g-кванта в еди­ницах массы превышает сумму масс покоя электрона и позитрона, т. е. энергетический порог такого превращения 1,02 Мэв. Образова­ние пары g-квантом в вакууме невозможно, так как не будет выпол­няться закон сохранения импульса. Закон сохранения энергии в этом процессе следует записать с учетом энергии ядра отдачи Е_A (или электрона отдачи):

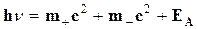(2.14)

где m₊c² и m_с² — полные энергии позитрона и электрона. Если же предположить, что g-кванты образуют пары в вакууме, закон со­хранения энергии запишется в виде hn= m₊c² + m_с²

Суммарный импульс электрона и позитрона максимален, когда они оба движутся в направлении g-кванта. Тогда

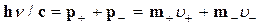
Предыдущее и последнее выражения совместны лишь при u₊=u_-=c, а это значит, что рождение g-квантом пары электрон — позитрон в вакууме возможно формально лишь при hn®¥.

Оценим энергию ядра отдачи при рождении пары. Максимальная энергия отдачи будет в том случае, если электрон и позитрон вылета­ют относительно направления g-кванта под углами 90° и угол между их направлениями движения 180°. При этом импульс ядра отдачи равен импульсу g-кванта, т. е. hn/c == Mu, где М — масса ядра; u— его скорость, а энергия ядра отдачи (максимально возмож­ная) E_A= (hn)²/ (2Mс²). Выражая энергию в мегаэлектронвольтах, получаем

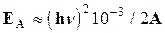, Мэв

Для g-квантов с энергиями, меньшими примерно 10 Мав, и для А>10E_A<5кэв. При образовании пары в поле электрона при тех же условиях его энергия отдачи может быть значительно больше 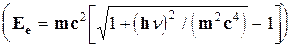Последнее обстоятельство поз­воляет выделять в эксперименте случаи рождения пары электрон — позитрон в поле электрона. В таких случаях в трековых приборах (например, в камере Вильсона) видны характерные триплеты (три трека, начало которых в одной точке).

Сечение образования пар на электронах и ядрах атома пропор­ционально Z² и довольно сложным образом зависит от энергии. Ти­пичные зависимости s_п от энергии приведены на рис. 2.6. Вначале сечение образования пар растет очень быстро, затем рост замедляется и при очень больших энергиях 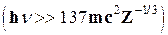сечение дости­гает постоянного значения, различного для материалов с разными Z:

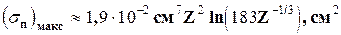
(2.15)

Энергия g-кванта распределяется почти равновероятно между электроном и позитроном. Однако с ростом энергии g-квантов пре­обладающим становится асимметричное распределение энергии. Сле­дует отметить, что спектры электронов и позитронов несколько от­личаются, если принять во внимание, что при удалении от ядра, в поле которого образовалась пара, электроны испытывают торможе­ние, а позитроны—ускорение. Этот эффект тем больше, чем выше атомный номер ядра и меньше энергия g-кванта.

Компоненты пары — электрон и позитрон — при больших энер­гиях g-квантов испускаются в направлении их движения в пределах углов по порядку величин, равных mc²/ (hn). При низких энергиях угловое распределение менее анизотропно и зависит от Z атома.

При регистрации g-квантов по эффекту образования пар имеет существенное значение то, что позитроны через очень короткое вре­мя аннигилируют, испуская два фотона с энергией 0,51 Мэв. Анни­гиляция имеет наибольшую вероятность при малых энергиях по­зитронов, поэтому угол между направлениями аннигиляционных квантов равен 180°.

Многократное рассеяние g-квантов. Рассмотренные выше основ­ные процессы взаимодействия g-излучения с атомами и электронами вещества приводят к изменению направления движения квантов, к изменению их энергии, образованию электронов и позитронов с непрерывным спектром энергий, которые, в свою очередь, создают тормозное и аннигиляционное излучение. Поэтому в целом картина прохождения g-квантов в веществе оказывается весьма сложной и может значительно отличаться от простого экспоненциального за­кона, который справедлив лишь для g-квантов, не претерпевших ни одного соударения.

Чаще всего g-кванты регистрируют и определяют их энергию по образованным ими электронам в детекторе. Поскольку в результа­те взаимодействия g-кванты могут передавать разную долю своей энергии электронам, то измерение энергии g-квантов по электронам требует сложного анализа.

Фотоядерные реакции. При поглощении g-квантов ядрами по­следние оказываются в возбужденных состояниях. Если энергия возбуждения выше энергии связи протона или a-частицы в ядре или если энергия возбуждения выше порога деления, то возможны (g, a)-, (g, ¦)-реакции с испусканием заряженных частиц и другие. Использование этих реакций для регистрации g-излучения ограни­чивается сравнительно малыми сечениями фотоядерных реакций по сравнению с аналогичными реакциями, вызываемыми нейтронами.

Наибольший практический интерес представляет реакция фото­расщепления дейтона (ядра дейтерия). Эта реакция, как и все фотоядерные реакции, пороговая с энергетическим порогом 2,23 Мэв. Сечение реакции фо­торасщепления дейтона имеет максимальное значение при энергии g-излучения около 4 Мэв и равно примерно 2 • 10^-27 см².

Энергии протонов, появляющихся при фоторасщеплении дейтонов, слабо зависят от угла их вылета. Различие в энергиях протонов, движущихся под 0 и 180° относительно направления движения g-кванта, мало: максимальный разброс составляет около (hn)²/ (4 М_dс²) (в знаменателе M_d — масса дейтрона).