Свойства равномерно сходящихся рядов.
До сих пор при изучении последовательностей и рядов функций эти функции предполагались заданными на произвольном множестве 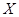 . Теперь мы перейдем к изучению свойств непрерывности, дифференцируемости, в связи с чем на множество
. Теперь мы перейдем к изучению свойств непрерывности, дифференцируемости, в связи с чем на множество 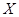 будут накладываться различные ограничения.
будут накладываться различные ограничения.
| Если функции 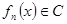 , , 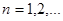 , , 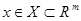 непрерывны в т. непрерывны в т. 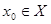 и ряд и ряд 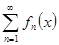 равномерно сходится на равномерно сходится на 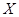 , то его сумма , то его сумма
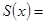 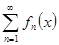 также непрерывна в т.
также непрерывна в т. 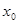 . .
|
Доказательство:
Зафиксируем произвольно 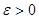 . Пусть
. Пусть 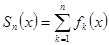 ,
, 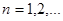 - частичные суммы ряда. По условию теоремы
- частичные суммы ряда. По условию теоремы 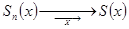 . Это значит, что существует такой номер
. Это значит, что существует такой номер 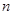 , что для всех точек
, что для всех точек 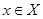 выполняется неравенство:
выполняется неравенство: 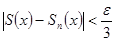 .
.
Зафиксируем номер 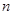 . Функция
. Функция 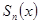 , являясь конечной суммой непрерывных (по условию теоремы) в т.
, являясь конечной суммой непрерывных (по условию теоремы) в т. 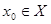 функций
функций 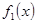 ,
, 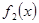 ,…,
,…, 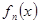 , сама непрерывна в этой точке. Поэтому
, сама непрерывна в этой точке. Поэтому 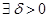 , что для всех точек
, что для всех точек 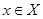 , удовлетворяющих
, удовлетворяющих 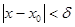 , выполняется неравенство:
, выполняется неравенство:
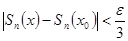
в силу этого для 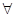 т.
т. 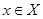
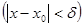 имеем:
имеем:
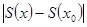 =
= 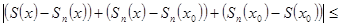
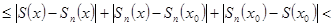
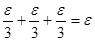 .
.
Это и означает непрерывность функции 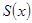 в т.
в т. 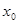 .
.
В условиях теоремы в т. 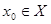 для ряда
для ряда 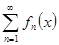 возможен почленный переход к пределу, т.е.
возможен почленный переход к пределу, т.е.
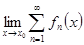 =
= 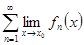 .
.
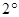
| Пусть функции 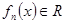 , , 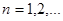 , , 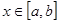 непрерывны на непрерывны на 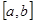 и ряд и ряд 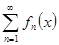 равномерно сходится на этом отрезке. Тогда, какова бы ни была точка равномерно сходится на этом отрезке. Тогда, какова бы ни была точка 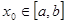 , ряд , ряд
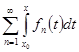 (6)
также равномерно сходится на (6)
также равномерно сходится на 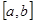 и и
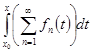 = = 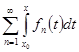 (Равенство означает, что в условиях этой теоремы ряд можно почленно интегрировать).
(Равенство означает, что в условиях этой теоремы ряд можно почленно интегрировать).
|
Доказательство:
В силу равномерной сходимости ряда и непрерывности его членов на 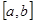 его сумма
его сумма
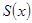 =
= 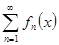
также непрерывна на этом отрезке (свойство 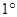 ), а
), а 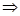 , и интегрируема по Риману на любом отрезке с концами в точках
, и интегрируема по Риману на любом отрезке с концами в точках 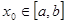 и
и 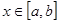 .
.
Покажем, что ряд (6) равномерно сходится к функции
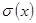 =
= 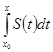
Как всегда, положим
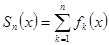 ,
, 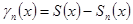
а через 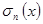 обозначим частные суммы ряда (6)
обозначим частные суммы ряда (6)
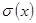 =
= 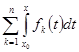 =
= 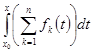 =
= 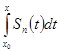
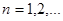
Имеем
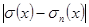 =
= 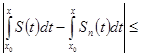
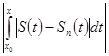 =
= 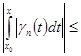
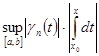 =
=
= 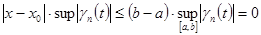
Т.е. 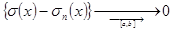 ,
, 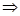 ряд (6) равномерно сходится на отрезке
ряд (6) равномерно сходится на отрезке 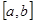 и его сумма равна
и его сумма равна 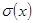 :
: 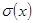 =
= 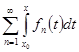 или
или
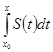 =
= 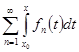
| Пусть функции 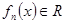 , , 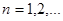 непрерывно дифференцируемы на непрерывно дифференцируемы на 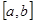 и ряд, составленный из их производных: и ряд, составленный из их производных:
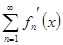 равномерно сходится на отрезке
равномерно сходится на отрезке 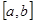 . Тогда, если ряд . Тогда, если ряд
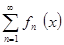 сходится хотя бы в одной точке
сходится хотя бы в одной точке 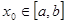 , то он сходится равномерно на всем отрезке , то он сходится равномерно на всем отрезке 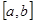 , его сумма , его сумма
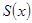 = = 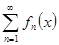 является непрерывно дифференцируемой функцией и
является непрерывно дифференцируемой функцией и
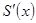 = = 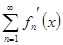
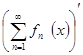 = = 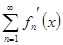
|
Доказательство:
Положим 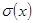 =
= 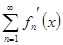
По свойству 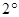 этот ряд можно почленно интегрировать:
этот ряд можно почленно интегрировать:
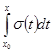 =
= 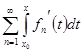 =
= 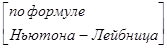 =
= 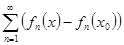 . – этот ряд в силу свойства
. – этот ряд в силу свойства 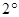 равномерно сходится на
равномерно сходится на 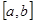 .
.
По условию теоремы числовой ряд 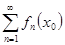 сходится, причем равномерно. Сумма двух равномерно сходящихся на
сходится, причем равномерно. Сумма двух равномерно сходящихся на 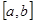 рядов:
рядов:
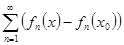 +
+ 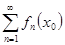 =
= 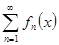
также, очевидно, равномерно сходится на 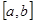 . В силу этого формулу можно записать в виде
. В силу этого формулу можно записать в виде
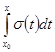 =
= 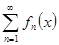 -
- 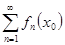 или
или 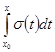 =
= 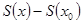 .
.
Функция 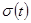 является суммой равномерно сходящегося ряда непрерывных функций на
является суммой равномерно сходящегося ряда непрерывных функций на 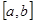 , и поэтому она сама непрерывна на этом отрезке, а тогда функция
, и поэтому она сама непрерывна на этом отрезке, а тогда функция 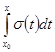 непрерывно дифференцируема на
непрерывно дифференцируема на 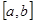 и
и
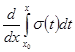 =
= 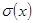
Это и означает, что функция 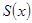 непрерывно дифференцируема и что
непрерывно дифференцируема и что
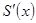 =
= 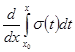 =
= 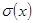 =
= 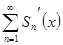 .
.
Дата добавления: 2015-08-14; просмотров: 595;
