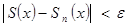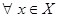Функциональные ряды.
| Опр. | Функциональным называется ряд 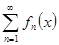 , где , где 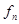 - последовательность функций на множестве - последовательность функций на множестве 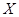 . .
|
| Опр. | Множество 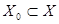 тех значений тех значений 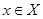 , для которых функциональный ряд сходится, называется областьюсходимости этого ряда. , для которых функциональный ряд сходится, называется областьюсходимости этого ряда.
|
При каждом фиксированном значении 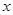 функциональный ряд превращается в числовой, поэтому для определения области сходимости используются признаки сходимости числовых рядов.
функциональный ряд превращается в числовой, поэтому для определения области сходимости используются признаки сходимости числовых рядов.
Пример 1 Определить область сходимости ряда 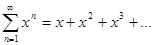
Решение:
1) 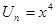
2) Применим признак Коши: 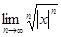 =
= 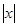 .
.
3) Поэтому при 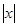 <1 – ряд сходится,
<1 – ряд сходится,
при 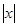 >1 – ряд расходится.
>1 – ряд расходится.
Ответ: область сходимости 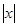 <1 или
<1 или 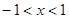 .
.
Равномерная сходимости функциональных последовательностей и рядов.
| Опр. | Функциональная последовательность 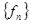 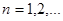 называется равномерно сходящейся к функции называется равномерно сходящейся к функции 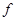 на множестве на множестве 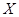 , если для , если для 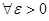 существует такой номер существует такой номер 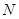 , что для всех точек , что для всех точек 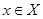 и всех номеров и всех номеров 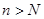 выполняется неравенство: выполняется неравенство: 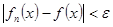 (1) (1)
|
|
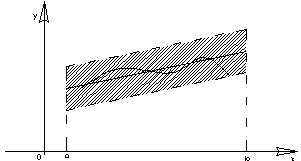
| Теорема (Критерий Коши равномерной сходимости последовательности) | Для того чтобы последовательность 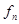 равномерно сходилась на множестве равномерно сходилась на множестве 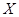 к некоторой функции, к некоторой функции, 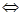 , чтобы для , чтобы для 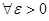 существовал такой номер существовал такой номер 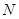 , что для всех , что для всех 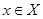 , всех , всех 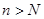 и всех и всех 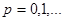 выполнялось неравенство: выполнялось неравенство: 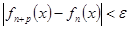
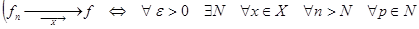
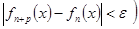 (2) (2)
|
Доказательство:
I (Необходимость  ). Пусть
). Пусть 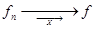 . Зафиксируем произвольно
. Зафиксируем произвольно 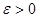 . Для него существует такой номер
. Для него существует такой номер 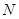 , что для всех
, что для всех 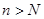 и всех
и всех 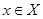 выполняется неравенство:
выполняется неравенство:
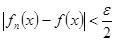 .
.
Поэтому для всех точек 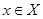 , всех номеров
, всех номеров 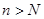 и всех
и всех 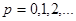 имеем:
имеем:
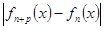 =
= 
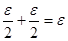
т.е. выполняется условие (2)
II (Достаточность  ). Пусть выполняется
). Пусть выполняется 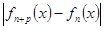
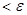 , тогда в каждой точке
, тогда в каждой точке 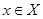 последовательность
последовательность 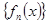 удовлетворяет критерию Коши сходимости числовых последовательностей и,
удовлетворяет критерию Коши сходимости числовых последовательностей и,  , сходится. Обозначим предел последовательности
, сходится. Обозначим предел последовательности 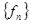 на множестве
на множестве 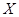 через
через 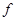 :
: 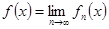 ,
, 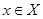 (3)
(3)
Перейдем к пределу в неравенстве (2) при 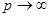 . В силу (3) получим, что для всех
. В силу (3) получим, что для всех 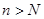 и всех точек
и всех точек 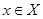 выполняется неравенство:
выполняется неравенство: 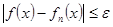 , т.е. последовательность
, т.е. последовательность 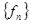 сходится равномерно ч. т.д.
сходится равномерно ч. т.д.
| Опр. | Ряд 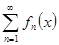 , , 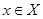 , называется равномерно сходящимся на множестве , называется равномерно сходящимся на множестве 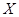 , если на , если на 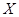 равномерно сходится последовательность его частичных сумм. равномерно сходится последовательность его частичных сумм.
|
Т.е., если 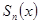 =
= 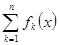 ,
, 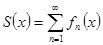 , то равномерная сходимость ряда означает, что
, то равномерная сходимость ряда означает, что 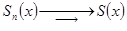 .
.
| Теорема (необходимое условие равномерной сходимости ряда) | Если ряд 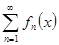 равномерно сходится на множестве равномерно сходится на множестве 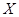 , то последовательность его членов равномерно стремится к нулю на этом множестве. , то последовательность его членов равномерно стремится к нулю на этом множестве.
|
Доказательство:
В самом деле, 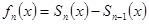 ,
, 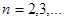 (4)
(4)
В случае равномерной сходимости на множестве 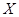 ряда последовательности
ряда последовательности 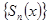 и
и 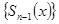 его частичных сумм равномерно стремится на
его частичных сумм равномерно стремится на 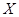 к его сумме
к его сумме 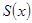 :
:
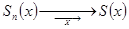 ,
, 
Поэтому 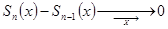 ,
,
а в силу (4) это означает, что 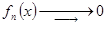 .
.
| Теорема (Критерий Коши равномерной сходимости ряда) | Для того чтобы ряд 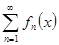 равномерно сходится на множестве равномерно сходится на множестве 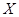 , ,  , чтобы для , чтобы для 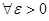 существовал такой номер существовал такой номер 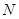 , что для всех , что для всех 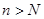 , всех , всех 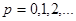 и всех и всех 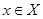 выполнялось неравенство: выполнялось неравенство:
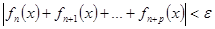
|
Доказательство:
В силу равенства 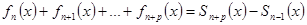 , где
, где 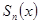 - частичные суммы рассматриваемого ряда, критерий Коши равномерной сходимости рядов следует из критерия Коши равномерной сходимости последовательностей.
- частичные суммы рассматриваемого ряда, критерий Коши равномерной сходимости рядов следует из критерия Коши равномерной сходимости последовательностей.
| Теорема (Признак Вейерштрасса) | Ряд 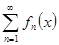 сходится абсолютно и равномерно на множестве сходится абсолютно и равномерно на множестве 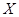 , если существует сходящийся ряд , если существует сходящийся ряд 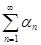 , такой, что , такой, что
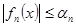 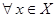 (Числовой ряд
(Числовой ряд 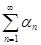 называется манорирующим (или мажорантой)). называется манорирующим (или мажорантой)).
|
Доказательство:
Т.к. ряд 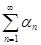 сходится и выполняется неравенство
сходится и выполняется неравенство 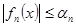
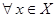 , то в силу признака сравнения ряд
, то в силу признака сравнения ряд 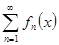 сходится абсолютно.
сходится абсолютно.
Докажем его равномерную сходимость. Зафиксируем 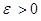 . В силу сходимости ряда
. В силу сходимости ряда 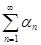 существует такой номер
существует такой номер 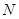 , что для всех
, что для всех 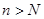 выполняется неравенство:
выполняется неравенство:
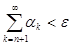
Обозначим 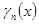 =
= 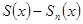 =
= 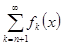 -
- 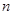 -ый остаток ряда. Тогда для всех
-ый остаток ряда. Тогда для всех 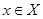 и
и 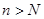 для остатков ряда
для остатков ряда 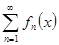 имеем:
имеем:
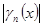 =
= 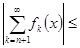
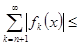
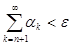 ,
,
т.е. 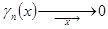 . Ряд сходится равномерно.
. Ряд сходится равномерно.
Пример. Исследовать на равномерную сходимость ряд: 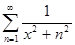
Решение:
При 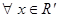 :
: 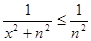 . Т.к. ряд
. Т.к. ряд 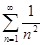 - сходится, то и ряд
- сходится, то и ряд 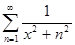 сходится абсолютно и равномерно.
сходится абсолютно и равномерно.
Дата добавления: 2015-08-14; просмотров: 925;

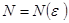 , что при
, что при