Первісна та її властивості.

РОЗДІЛ VI. НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ

Лекція 19

Первісна та її властивості.

Невизначений інтеграл та його властивості.

Метод заміни змінної

Однією із головних задач диференціального числення, з яким ми познайомилися у першому семестрі, є знаходження похідної заданої функції. Але багато задач техніки і природознавства вимагають виконання оберненої дії, а саме, вміння відновлювати функцію за її відомою похідною або диференціалом. Як відомо, цю обернену дію називають інтегруванням. У її основі лежать поняття первісної та невизначеного інтеграла.

Первісна та її властивості.

Означення 19.1.Функцію 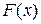називаютьпервісною для функції 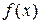на даному проміжку, якщо у кожній точці цього проміжку виконується рівність:

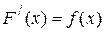
(19.1)

або, використовуючи символіку диференціалів,

.

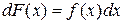(19.2)

Приклад 19.1. Визначити, для яких функцій 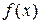функції:

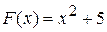
і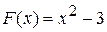

є первісними.

Розв’язання. Знайдемо похідні від заданих функцій:

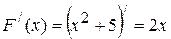
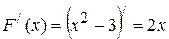
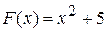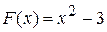Отже, обидві функції та є первісними для однієї і тієї самої функції 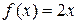. Очевидно, що для функції 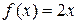можна назвати нескінченну множину первісних, але всі вони будуть складатися із 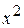і сталого доданка. Узагальнює це спостереження наступна теорема.

Теорема 19.1. Якщо 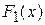і 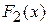є двома первісними для функції 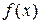на відрізку 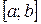, тоді різниця міжними дорівнює сталій величині.