Ряд - обобщенный гармонический ряд.
1. Исследовать на сходимость ряд: 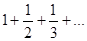 =
= 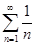 ,
, 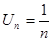
Необходимое условие №1 выполнено: 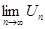 =
=  = 0.
= 0.
Докажем, что ряд расходится: Пусть 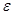 =
= 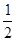 , p = n, тогда
, p = n, тогда
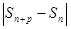 =
= 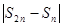 =
= 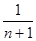 +
+ 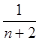 + … +
+ … + 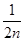 >
> 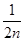 +
+ 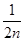 + … +
+ … + 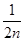 =
= 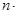
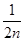 =
= 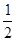 =
= 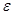
т.к. условие критерия Коши нарушено, то ряд расходится.
2. Исследовать на сходимость ряд 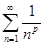 ,
, 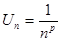 .
.
- если p 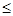 0, то
0, то 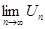
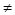 0 и ряд расходится
0 и ряд расходится
- если 0 < p 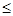 1,
1, 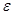 =
= 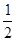 , p = n, то
, p = n, то
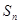 =
= 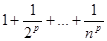 ,
, 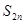 =
= 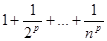 +…+
+…+ 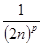 , и
, и
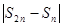 =
=  +…+
+…+ 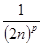 >
> 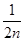 +
+ 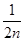 + … +
+ … + 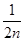 =
= 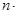
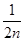 =
= 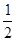 =
= 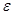
т.к. условие критерия Коши нарушено, то ряд расходится.
- если p >1, то
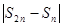 =
=  +
+ 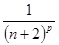 +…+
+…+ 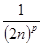
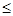
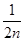 +
+ 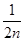 + … +
+ … + 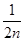 =
= 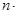
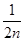 =
= 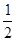 =
= 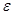
Ряд сходится.
Дата добавления: 2015-08-14; просмотров: 1446;
