Элементарные оценки потерь энергии заряженной частицей.

Рассмотрим прохождение через вещество тяжелой (M >> me) нерелятивистской ( V<< c) заряженной (ze) частицы. Предположим, что эта частица имеет достаточно высокую скорость ( 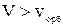) , чтобы считать все атомные электроны свободными.
Итак: тяжёлая нерелятивистская заряженная частица с зарядом ze и скоростью v, пролетает вдоль оси x на расстоянии b от электрона.

На рисунке красным кружком изображен не электрон, а любая заряженная частица с зарядом Ze.

В приближении малых углов рассеяния (q << 1)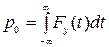

Электрическое поле частицы

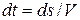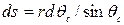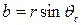, , и

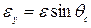
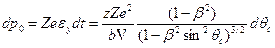
Интегрирование по 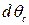от 0 до p дает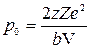

Переданная энергия Т =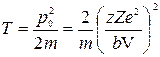

Или (если учесть, что тяжелая заряженная частица пролетает мимо электрона среды и заряд электрона Ze = e)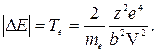

z (маленькое) – заряд пролетающей частицы в единицах заряда электрона

3. Среда наполнена атомами, атомные оболочки заполнены электронами (Z – электронов на атом).

Плотность среды - ρ г/см³,

плотность атомов: nат= ρ·NА/A см^-3, где NА-число Авогадро,

плотность электронов: ne =Z·nат= Z/A ·ρ·NАсм^-3 .

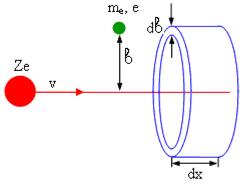
Если частица проходит в среде путь dx, то она взаимодействует почти одинаково со всеми электронами, которые располагаются на одном и том же расстоянии b от ее траектории, и каждому из них передает энергию Te. Количество таких электронов на пути dx будет

определяться плотностью электронов и объемом кольцевого цилиндра длиной dx с внутренним радиусом b и внешним радиусом b+db . Объем этого цилиндра – 2πbdbdx. Электронов в нем будет:

ne=2pbdbdx×Z nат.

Каждому из этих электронов пролетающая частица передает

энергию DE, а всем электронам, находящимся на расстоянии b от нее в слое db на пути dx, частица передает энергию

.

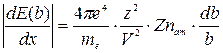Энергия частицы при этом взаимодействии уменьшается, и поэтому производная dE(b)/ dx

отрицательна.

4. Чтобы найти ионизационные потери частицы на пути dx со всеми электронами среды, с которыми она взаимодействует с разными параметрами удара, надо проинтегрировать по всем возможным параметрам удара от bmin до bmax:

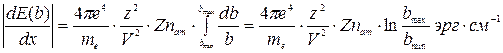
Пределы интегрирования должны быть конечны, так как из самых общих физических соображений удельные потери энергии (потери энергии на единицу длины пути) dE/dx должны иметь конечную величину - частица с конечной энергией не может потерять бесконечно большую энергию. Отсюда следует, что bmin≠0 и bmax≠ ∞. Рассмотрим, какими факторами

определяются величины предельных параметров удара bmin и bmax.

Bmin

Минимальному значению параметра удара соответствует максимальная передаваемая энергия. Ранее был получено соотношение, связывающее передаваемую электрону

энергию с параметром удара b: Te = | DE | = 2 z²e⁴⁄ (meV² b² ).

Откуда имеем: b² = 2z²e⁴ ⁄ meV² · 1 ⁄ DE и, следовательно,

b²min= 2z²e⁴ ⁄ meV² · 1⁄ DEmax.

Если сталкиваются две частицы с массами М и me и M » me,

то максимальная передаваемая энергия будет:

.

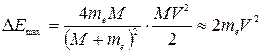Следовательно:

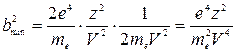и .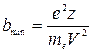

В релятивистском случае в выражении для bmin появляется коэффициент 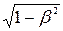, так как максимальная передаваемая энергия будет расти со скоростью частицы:

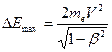, а .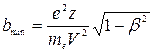

Итак, мы получили выражение для bmin с точки зрения классического подхода.

Можно найти минимальный параметр удара b′min с помощью квантово-механичеcкого

подхода, используя для этого соотношение неопределенностей .

Так как ,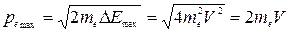

то для b′min получаем:

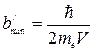в нерелятивистском случае

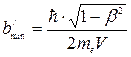в релятивистском случае.

Обычно b′min > b min , поэтому используется классическое

выражение для bmin.

Bmax

Чем больше параметр удара, тем меньше передаваемая электрону энергия DEmin.

bmax соответствует случаю, когда передаваемая энергия близка к энергии связи этого электрона с ядром. Поскольку энергия связи разных электронов атома различна, то вводится обычно некоторая усредненная характеристика энергии связи электронов в атомах данного элемента (A,Z), называемая средним потенциалом ионизации I .

Для разных элементов I = I0·Z , где I0 слабо зависит от Z вещества.

В табл. приведены значения I0 для некоторых элементов.

Выбираем в качестве максимального прицельного параметра такой, при котором электрону передается энергия, равная среднему потенциалу ионизации: DEmin = I. Так как

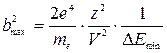, то .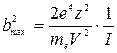

Теперь можно найти выражение для .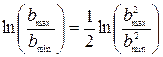

Подставляя найденные нами значения bmax и bmin , получаем:

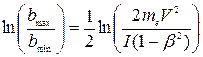
Выражение для удельных ионизационных потерь энергии частицы

(или линейная тормозная способность вещества):

приобретает вид:

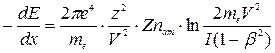- формула Бора