ЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ

Э/М вз-ие существует между всеми частицами, имеющими электрический заряд и фотонами. Э/М вз-ие – это или результат обмена фотонами в момент взаимодействия или результат поглощения или испускания фотонов.

Константы связи - величины, характеризующие силы взаимодействия частиц или полей.

Эти константы обычно выбираются безразмерными и обозначаются через αe, αw, αs.

В элементарные амплитуды непосредственно входят квадратные корни из этих величин:
(αe)^1/2 - в элементарную амплитуду электромагнитного взаимодействия;
(αw)^1/2 - в элементарную амплитуду слабого взаимодействия;
(αs)^1/2 - в элементарную амплитуду сильного взаимодействия.

Константа Э/М взаимодействия определяет интенсивность процесса - a = .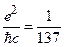

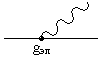- узел электромагнитного взаимодействия

g_эл (множитель, входящий в элементарную амплитуду)

g_эл = (a)^1/2 = (e²/ c)^1/2 = (1/137)^1/2 0.1,

Для описания различных процессов с участием частиц используют диаграммы Фейнмана. На этих диаграммах линиям со свободными концами отвечают реальные частицы или ядра, а внутренним линиям - виртуальные частицы. Точка, в которой рождается и поглощается виртуальная частица, называется узлом диаграммы. Узлы диаграммы содержат основную информацию о процессе - типе фундаментального взаимодействия и его вероятности.

Линиям виртуальных частиц сопоставляются функции распространения этих частиц, называемые пропагаторами. Пропагатор для частицы, переносящей взаимодействие и

имеющей массу m ¹ 0, равен 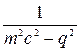, где q - четырехмерный импульс частицы.

Пропагатор входит множителем в амплитуду вероятности процесса. Для того, чтобы рассчитать вероятность (сечение) процесса, необходимо прежде всего нарисовать для него все возможные диаграммы, и вычислить амплитуду вероятности для каждой диаграммы.

Дифференциальное сечение процесса пропорционально квадрату модуля амплитуды соответствующего процесса. (Амплитуда процесса- амплитуда перехода между двумя состояниями системы, является матричным элементом оператора, описывающего процесс,

напр. рассеяния.)

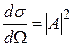
Полная вероятность процесса равна квадрату модуля суммарной амплитуды для всех возможных диаграмм.

Диаграммы содержат алгоритм расчета амплитуды процесса.

Амплитуды вероятности испускания (поглощения) частицы, которое происходит в результате определенного взаимодействия, пропорциональна константе g, которая равна корню из

константы связи.

Для электромагнитного взаимодействия соответствующая константа равна корню квадратному из постоянной тонкой структуры

gэл(константа связи) = .

Для диаграмм с N узлами амплитуда пропорциональна g^N.

Вероятность (сечение) процесса пропорциональна квадрату амплитуды.

, или .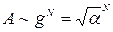

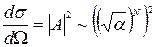
Если в Э/М процессе участвует одинфотон (или одна вершина), то вероятность такого процесса пропорциональна a ,

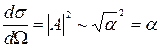
если двафотона (или две вершины) вероятность такого процесса пропорциональна - a² :

ПРИМЕР: Оценить отношение сечений двух- и трехфотонной аннигиляции электрон-позитронной пары.

В случае двухфотонной аннигиляции фейнмановская диаграмма имеет две вершины, поэтому сечение этого процесса можно оценить так -

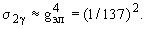
В случае трехфотонной аннигиляции фейнмановская диаграмма имеет три вершины, и сечение этого процесса пропорционально

То есть отношение сечений

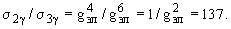
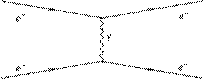
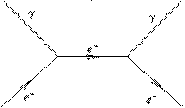
ПРИМЕР: Нарисовать диаграммы Фейнмана для следующих процессов: 1) рассеяние электрона на электроне; 2) эффект Комптона; 3) электрон-позитронная аннигиляция; 4) фотоэффект в кулоновском поле ядра; 5) образование электрон- позитронной пары в кулоновском поле ядра.

1) Рассеяние электрона на электроне. Виртуальная частица - фотон.

2) Эффект Комптона. Виртуальная частица - электрон.

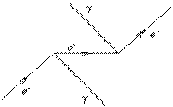
3) Электрон-позитронная аннигиляция. Виртуальная частица - электрон или позитрон.

4) Тормозное излучения электрона в поле ядра

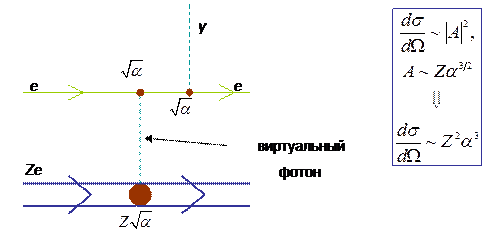
5) Фотоэффект в кулоновском поле ядра. Виртуальная частица - фотон.

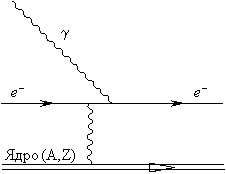
6) Образование электрон-позитронной пары в кулоновском поле ядра. Виртуальная частица - фотон.

Особый класс взаимодействийсоставляют процессы, излучения Э/М волн при равномерном движении частиц в среде с показателем преломления n > 1 -- излучение Вавилова-Черенкова. (ИЗЛУЧАЕТ СРЕДА)

Кроме того, существует переходное излучение, возникающее при пересечении равномерно двигающейся заряженной частицы границы раздела двух сред с разными показателями преломления.

Простейшие задачи и оценки.

Задача 1. На основании простейшей концепции Нильса Бора оценить скорости «вращения» электронов в атоме и радиусы электронных орбит.

Ответы: 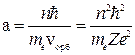. Т.е. скорость «вращения» электронов в атоме убывает с увеличением главного квантового числа n , а радиус орбиты вращения электронов в атоме пропорционален n².

Задача 2. Найти энергию связи электрона в атоме eсв .

Ответ. Энергия связи электрона с ядром eсв , т.е. потенциальная энергия электрона на орбите равна

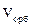, а ² = .

В общем случае для электронных орбит в атомах имеем:

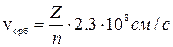и .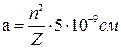

Чтобы произошла ионизация, т.е.электрон мог покинуть атом, надо, чтобы при взаимодействии

с пролетающей мимо заряженно частицей этот электрон получил кинетическую энергию Те большую, чем энергия связи его с атомом, т.е. Те > ecв.

Задача 3. Определить минимальную кинетическую энергию Е и скорость V пролетающей частицы, необходимую для ионизации атома среды.

Ответ. Е 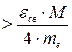и .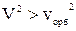

Если энергия, передаваемая электрону Те много больше энергии связи этого электрона ecв

(Те >> ecв) , т.е. энергия пролетающей частицы Е 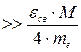, то электроны атома можно рассматривать как свободные и покоящиеся по сравнению с летящей частицей.

Элементарные электромагнитные процессы можно классифицировать с точки зрения классической физики на основе представлений о параметре удара (прицельном параметре, параметре соударения) b , т.е. расстоянии наибольшего сближения частиц.

При взаимодействии частиц с атомами среды имеет смысл проводить сопоставление параметра удара b с размером атома a.

В зависимости от того, как соотносятся между собой величины b и a происходит тот или иной процесс взаимодействия.