РАСЧЕТ СОЕДИНЕНИЙ

Основная задача расчета состоит в определении требуемого натяга и соответствующей ему посадки (ГОСТ 25347 — 82) для передачи сдвигающей нагрузки от вра­щающего момента или осевой силы.

Возможны случаи, когда посадка не может быть реали­зована в конструкции по условиям прочности (обычно охватывающей детали). Поэтому при проектировании соеди­нений должны быть обеспечены как требования неподвиж­ности (неразбираемости) соединения, так и условия проч­ности его деталей.

Условие совместности перемещений сопряженных деталей. Предположим, что в результате сборки охватывающая де­таль 2 (втулка) запрессована на охватываемую деталь 1 (рис. 31.2). Тогда в результате деформации произойдет ра­диальное перемещение точек поверхностей деталей 1 и 2 соответственно на величины 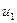и , и 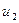радиальный натяг будет скомпенсирован этими перемещениями, т. е.

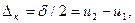(31.1)

где 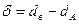— диаметральный натяг, равен разности по­садочных диаметров d_B и d_A деталей (см. рис. 31.2).

Уравнение (31.1) отражает геометрическую сторону задачи.

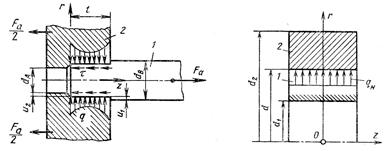
Рис. 31.2. Схема к расчету Рис. 31.3. Расчетная схема

соединения натягом соединения с натягом

Контактные напряжения в соединении. В зоне сопряжения деталей будут действовать контактные давления (радиальные напряжения) q, которые распределены по длине соединения (вдоль оси z) обычно существенно неравномерно (см. рис. 31.2, на котором показаны напряжения, действующие на деталь 1), так как равномерной деформации препятствуют выступающие части деталей.

В предварительном расчете (на этапе технического пред­ложения) полагают, что контактные давления одинаковы во всех точках поверхностей контакта. Это эквивалентно допу­щению о сопряжении двух цилиндров (толстостенных труб) одинаковой длины (рис. 31..3).

Задача о сопряжении с натягом двух толстостенных ци­линдров рассмотрена в курсе «Сопротивление материалов» (задача Ламе) [21]. Установлено, что радиальные перемещения точек контакта

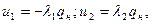(31.2)

где 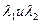— коэффициенты радиальной податливости де­талей / и 2; q_H — номинальное контактное давление.

Смещение и_х считают отрицательным, так как оно проис­ходит в направлении, противоположном направлению оси r.

Соотношения (31.2) отражают физическую сторону задачи.

Коэффициенты радиальной податливости зависят от ра­диальных размеров и материалов деталей

(31.3)

В равенствах (31.3) обозначено: d — посадочный диаметр; E_lt Vi и Е₂, v₂ — модуль упругости и коэффициент Пуассона соответственно для охватываемой 1 и охватывающей 2 де­талей (см. рис. 31.3); 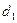— диаметр отверстия в охватываемой детали 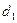= 0 — для сплошного вала); d₂ — наружный диаметр охватывающей детали.

Учитывая равенства (31.1) и (31.2), несложно получить

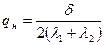(31.4)

Отметим, что натяг 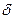в этом равенстве является рас­четным и соответствует разности посадочных диаметров де­талей с идеально гладкими поверхностями.