РАСЧЕТ НА ПРОЧНОСТЬ ЧЕРВЯЧНЫХ ПЕРЕДАЧ

Расчет проводят для определения размеров передачи, обеспечивающих безотказную (по условиям прочности) работу в течение ресурса.

Усилия зацепления. При определении усилий полагают, что главный вектор (равнодействующая) F_n контактных давлений, действующих на площадках контакта зубьев, приложен в полюсе П и направлен по линии зацепления (см. рис. 21.4).

Окружное усилие F_t1 на червяке бу­дет осевым усилием F_a2 для колеса (рис. 21.7)

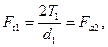
а окружное усилие F_t2 наколесе будет осевой силой F_a1 для червяка

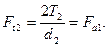
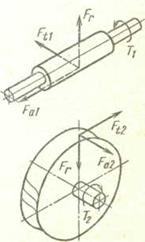
Рис. 21.7. Усилия в зацеплении червячной передачи

Радиальное усилие на колесе и червяке (F_r1 = F_r2)

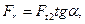
а нормальное усилие

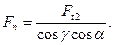
Расчетная нагрузка.Поаналогии с расчетом косозубой передачи (см. с. 340 и 341) номинальная удельная нагрузка для червячной передачи

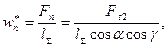
где 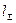— суммарная длина контактных линий. Расчетная удельная нагрузка

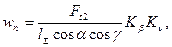(21.2)

где 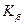— коэффициент неравномерности нагрузки; K_v — коэффициент динамической нагрузки, при скорости скольжения v_CK 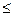3 м/с K_v 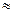1.

Хорошая прирабатываемость материалов колес уменьшает неравномерность распределения нагрузки по контактным линиям.

В предварительных расчетах передач можно принимать произведения 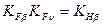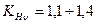(большие значения для высокоскоростных передач и при переменной нагрузке).

Виды повреждений передач.Основные виды повреждений червячных передач:

а) поломка зубьев колеса;

б) контактное повреждение рабочих поверхности из-за усталости или заедания;

в) износ зубьев червячного колеса.

Расчет и определение размеров передачи выполняют из условия предотвращения усталостных повреждений.

Расчет зубьев колеса на прочность приизгибе. Витки червяка на прочность не рассчитывают, так как материал червяка, как правило, значительно прочнее материала колеса. При расчете используют те же допущения и соотношения, что и при расчете косозубых колес, с соответствующими поправками, учитываю­щими особенности формы зубьев и положение контактных линий.

Учитывая, что для червячного зацепления коэффициент 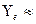0,74 и коэффициент 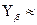0,93 (для среднего значения угла 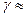10°), условие прочности (20.25) примет в рассматриваемом случае вид ( 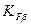K_Fv =1)

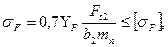(21.3)

где т_п = m cos 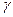— модуль в нормальном сечении; Y_F - коэф­фициент формы зуба, принимают по эквивалентному числу зубьев z_v = z₂/cos³ 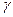(какдля косозубых колес, см. с. 334):

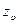......24 28 30 32 35 37 40 50 60 80 100

Y_F.....1,88 1,80 1,76 1,71 1,64 1,61 1,55 1,45 1,40 1,34 1,3

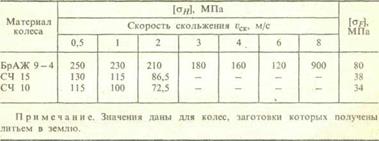
Допускаемые напряжения изгиба для зубьев колеса опре­деляют так же, как и для зубчатых колес. Приближенные зна­чения [ 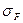] даны в табл. 21.2.

Таблица 21.2. Допускаемые напряжения для червячных передач

Расчет зубьев колеса на контактную прочностьосновывается на условии прочности поверхностных слоев зубьев по до­пускаемым контактным напряжениям (см. с. 353).

Учитывая, что радиус кривизны профиля витка в нормаль­ном сечении , получаем следующее соотношение для приведенной кривизны:

(21.4)

Подставляя в формулу (19.3) соотношение (21.2) для расчет­ной удельной нагрузки, выраженное через вращающий момент на колесе Т₂ (Н • м), и равенство (21.4), принимая далее: 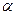= 20°; 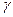=10°; 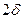=100°; 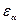=1,8; Е₁ = 2,15 • 10⁵ МПа (для стали);

Е₂ =0,9 • 10⁵ МПа(для бронзы и чугуна); v = 0,3, после неслож­ных преобразований получим

(21.5)

Межосевое расстояние передачи, мм:

(21.6)

где 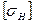— допускаемое напряжение для материала колеса.

Межосевые расстояния редукторов стандартизованы. Для «вписывания» червячной передачи в стандартное значение a_w колесо обычно изготовляют со смещением 1 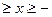1 (см. с. 328).