КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ И КПД ПЕРЕДАЧИ

Кинематические характеристики.Скорость относи­тельного перемещения гайки и винта, м/с:

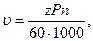
где z — число заходов винта; Р — шаг резьбы; п — частота вра­щения гайки или винта, об/мин.

Число заходов z = 1 назначают для самотормозящихся винтов; для несамотормозящихся механизмов принимают z = 2; 4 (см. ниже).

Вращение винта или гайки в механизмах осуществляется обычно с помощью маховика (рукоятки), шестерни и т. п., при этом передаточное отношение можно условно представить в виде отношения перемещений маховика S_мк соответствую­щему перемещению гайки (винта) S_Г:

где D — диаметр маховика (шестерни и т. п.); S = zP — ход винта.

Зависимость между окружной силой на маховичке F_M и осевой силой на гайке (винте) F_a найдем из равенства работ:

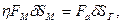
откуда

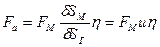, (22.1)

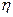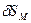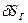где — КПД механизма; и — перемещения маховика и гайки.

При D = 200 мм, Р = 1,5 мм, z = 1 и 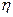= 0,5 F_а = 200 F_М и и 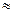420.

Таким образом, винтовая передача позволяет с малым вращающим моментом создать большую силу (получить выигрыш в силе) или осуществить медленные точные перемещения. Первое из указанных достоинств используют в домкратах, прессах и других устройствах, второе достоинство реализуют в регулировочных механизмах, механизмах подачи станков, механизмах управления механизацией крыльев летательных аппаратов и т. д.

Коэффициент полезного действия механизмов.Если винт 1 (рис. 22.1, б) нагружен осевой силой F_a, то для его поступа­тельного перемещения к маховичку 2 необходимо приложить момент 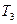, который будет расходоваться на преодоление сопротивления в резьбе 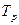и трение на опорном торце махо­вичка Т_T. Обычно момент трения на торце невелик, так как передачу осевой силы осуществляют через упорный подшип­ник, т. е. положим Т₃ = Т_р.

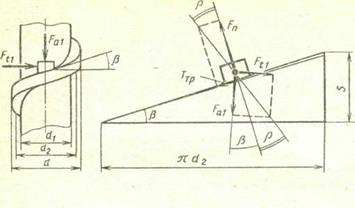
а)б)

Рис. 22.2. К определению КПД винтовой пары

Зависимость между ними можно установить из равенства работ за один оборот винта. Предположим, что нагрузка F_a равномерно распределена между витками прямоугольного сече­ния (F₁ — усилие на один виток). Тогда, переходя к одному витку (рис. 22.2, а), введем в рассмотрение его расчетную мо­дель в виде наклонной плоскости (рис. 22.2, б), угол подъема которой 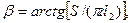где S и d₂ — ход и средний диаметр резьбы винта.

Если через F_tl обозначить окружную силу на одном витке и учесть, что реакция от гайки на винт будет наклонена к нормали под углом трения 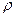= arctg f ( f- коэффициент трения, f =0,08 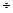0,12), то несложно установить

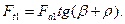
Из равенства работ за один оборот гайки

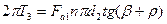
получим

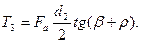
(22.2)

КПД механизма найдем как отношение работ на завинчи­вание винта без учета сил трения ( 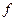= 0 и 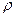= 0) и с учетом сил трения. Тогда из зависимости (22.2) следует

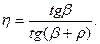(22.3)

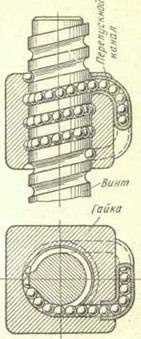
Рис. 22.3. Шариковинтовый механизм

Из формулы (22.3) видно, что КПД передачи возрастает с увеличением угла подъема 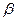и уменьшением коэффициен­та трения в резьбе (уменьшением ).

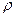Для увеличения угла подъема в вин­товых механизмах применяют много-заходные винты. Ход резьбы в этом случае S = Pz (Р и z — шаг и число заходов резьбы). Однако винты с 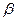> 25° на практике не применяют, так как дальнейшее увеличение 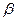не дает су­щественного повышения КПД, а пере­даточное отношение при этом снижа­ется. Обычно 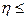0,7.

Для повышения КПД винтовых ме­ханизмов стремятся уменьшить коэф­фициент трения в резьбе путем изготов­ления гаек из антифрикционных материалов (бронзы, латуни и др.), смазывания трущихся поверхностей, тщательной обра­ботки контактирующих поверхностей.

В последние годы получили распространение шариковинтовые механизмы (рис. 22.3). В таких механизмах между витками винта и гайки размещаются шарики. При вращении винта шарики увлекаются в направлении его поступательного дви­жения, попадают в обводной канал в гайке и возвращаются в полость между винтом и гайкой. Механизмы имеют высокий КПД ( 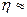0,9), так как коэффициент трения качения невелик ( 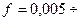0,01).