Оценки верхних границ корректирующих способностей кодов

Если расстояние между любыми двумя точками кода не меньше, чем 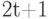, то шары радиуса с центрами в кодовых словах не пересекаются. Поэтому общее число точек в этих шарах равно: , где - число точек (кодовых слов) в коде 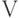, а 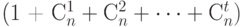число точек в шаре радиуса . Так как число точек, попавших в шары, очевидно, не превосходит общего числа точек (двоичных слов) в 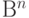, то . Это неравенство справедливо для любого множества с расстоянием между любыми двумя точками не меньше, чем 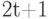, в том числе и для кода с максимальным числом слов 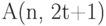, откуда и следует неравенство Хеминга.

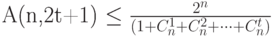
Для максимального числа слов 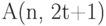в коде, исправляющем ошибок, может быть получена оценка снизу.

Утверждение (неравенство Варшамова - Гилберта):

Чтобы доказать неравенство Варшамова - Гилберта, можно рассмотреть следующую процедуру построения кода, исправляющего ошибок.

В качестве первого кодового слова возьмем произвольное слово (вектор) из 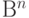. Рассмотрим шар радиуса 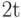с центром в данном слове. Если в 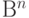есть слова, не вошедшие в этот шар, то в качестве второго кодового слова выберем любое из них. В качестве третьего кодового слова выберем любое слово, не вошедшее ни в один из построенных ранее шаров. Построим шар радиуса 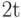с центром в данном слове. Продолжим эту процедуру выбора кодовых слов и построения шаров до тех пор, пока не будут исчерпаны все точки пространства 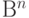. Предположим, построение кода завершилось за шагов. После завершения этой процедуры пространство 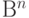будет покрыто построенными шарами, содержащими по 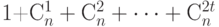точек каждый. Поскольку шары могут пересекаться, справедливо неравенство 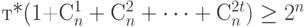. Центры шаров образуют код 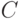, имеющий, как следует из способа построения, кодовое расстояние 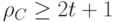. Из того, что - это максимально возможное число точек кода с кодовым расстоянием не меньше, чем 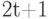, следует, что 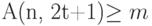и 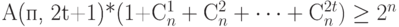. Последнее неравенство эквивалентно неравенству Варшамова - Гилберта.