Из уравнения Бернулли
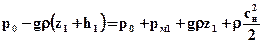 .
.
Здесь zм1— отметка положения вакууметра над точкой s.
Поэтому
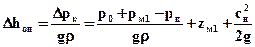 .
.
С другой стороны,
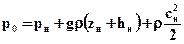 ,
,
откуда вакуумметрическая высота всасывания
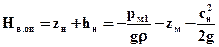 ,
,
где zм — отметка вакуумметра над осью подводящего трубопровода.
Подача, напор, мощность насоса и кавитационный запас в динамическом насосе приводятся к номинальной частоте вращения и плотности натуральной жидкости по формулам (3.5), (3.6), (3.7), причем Dh пересчитывается так же, как и H. Если измерялись частота ,fоп и напряжение Uопсети, то показатели приводятся к номинальной частоте fн и напряжению Uнпо тем же формулам, но отношение частот вращения заменяется величиной fн kэ /fоп, где
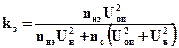 ,
,
где nнэ, nс— номинальная (по паспорту) и синхронная частоты вращения вала электродвигателя.
Относительные погрешности результатов:
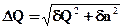 ;
; 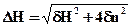 ;
;
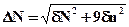
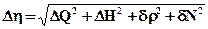 .
.
Результаты расчетов округляют до ряда R10 и сравнивают с допускаемыми значениями.
Характеристику насоса строят по приведенным значениям Q, Н (или Р) и N.Кривая допускаемого кавитационного запаса, вычисляемого по формуле (11.7), строится для приведенных значений Q в рабочем интервале подач.
Показатели надежности определяют по формулам математической статистики, используя рабочие графики всех насосов, участвовавших в определительных испытаниях.
Пусть dj — ресурс работы j-го насоса (суммарное время работы до капитального ремонта); Трi — время ремонта при i-м отказе; Тп— суммарное время на профилактику (смазка, подтяжка); m — число отказов всех Nнасосов; ti — время работы до i-го отказа для каждого насоса.
Опытная средняя «наработка на отказ» (время работы до отказа) и опытный средний ресурс:
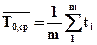 ;
; 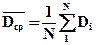 ,
,
Опытные среднеквадратичные отклонения «наработки на отказ» и ресурса:
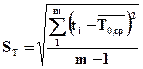 ;
; 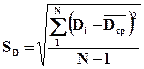 .
.
Опытные коэффициенты вариации тех же величин:
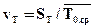 ;
; 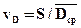 .
.
В зависимости от коэффициента вариации следует принимать распределение случайной величины: при v <: 0,35 — нормальное, при v > 0,35 — Вейбулла. Далее подсчитываются нижние доверительные границы «наработок на отказ» и ресурсов, включаемых в техническую документацию.
При нормальном распределении:
гамма-процентные
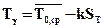 ;
; 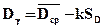 ;
;
средние
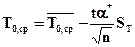 ;
; 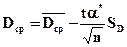 .
.
(здесь n = m) (здесь n = N)
При распределении Вейбулла соответственно:
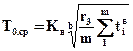 ;
; 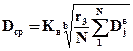 ;
;
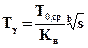 ;
; 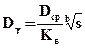 ,
,
где s определяется в зависимости от доверительной вероятности g:
g, % 75 90 95
s... 0,286 0,106 0,5
Величины 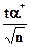 , k, r3 выбирают в зависимости от числа n, причем kзависит также от требуемого значения g, а коэффициенты распределения Вейбулла Кв и b— в функции vtи vd[1]
, k, r3 выбирают в зависимости от числа n, причем kзависит также от требуемого значения g, а коэффициенты распределения Вейбулла Кв и b— в функции vtи vd[1]
Коэффициент технического использования
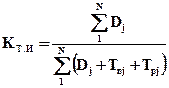 .
.
Пополученным показателям надежности определяют периодичность ремонтови потребность в запасных частях.
Дата добавления: 2015-07-10; просмотров: 443;
