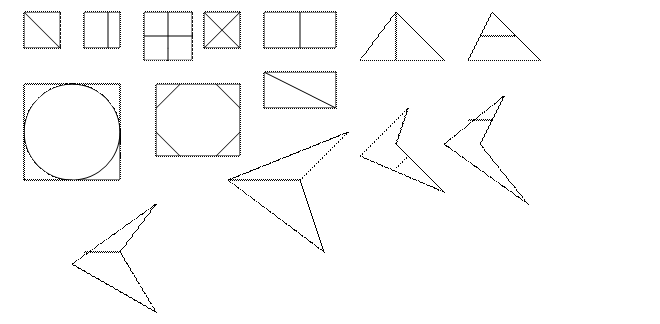
Основные приемы работы в младшем дошкольном возрасте

(ознакомление с кругом, квадратом, треугольником)

1. Предъявление геометрической фигуры с её называнием: это круг.

2. Многократное обведение контура геометрической фигуры пальцем в сопровождении слова, которое завершается скользящим движением ладони по всей поверхности фигуры.

3. Сравнение геометрических фигур между собой с выделением признаков их сходств и различий по цвету, размеру, наличию углов, сторон, вершин, их количеству, соотношению, направлению линий.

4. «Вырисовывание» контура геометрической фигуры в воздухе, на столе и т.п..

5. «Пробовательные» действия для выявления свойств геометрических фигур (прокатить, просунуть в отверстие).

6. Наложение моделей фигур друг на друга, их приложение сторонами.

7. Дидактические игры и упражнения.

I этап – 3-4 года

Цель: познакомить с понятием «круг», учить называть и различать круги по цвету и величине.

Знакомство начинается с предъявления двух кругов разного цвета и размера. - Что это? - Какого они цвета? Величины? Чем отличаются? Чем похожи?

Далее обвести пальцем по контуру, прорисовать, прокатить, наложить друг на друга и выполнить упражнения на закрепление (сложить картинку «Неваляшка», выложить «бусики» и т.п.).

II этап – 3-4 года

Цель: дать представление о квадрате, научить различать и называть круг и квадрат, упражнять в обследовании этих фигур.

Используем сюрпризное внесение круга и квадрата (одного цвета, подобранных таким образом, чтобы круг вписывался в квадрат). Сначала рассматривается круг, называются его признаки. Затем предъявляется квадрат и называется: «это квадрат». Дети сравнивают фигуры по цвету (одинаковые), размеру, форме (с углами и без углов), используя все обследовательские действия. Предлагаются упражнения на закрепление – различение и называние: «Дай такой же», «Подбери колёса к поезду», «Продолжи ряд», «Разложи правильно» и т.п.

Часто для повышения интереса и развития внимания используются стихотворные тексты, например:

Нет углов у меня, и похож на блюдце я,

На тарелку и на крышку, на кольцо, на колесо,

Кто же я такой, друзья? назовите вы меня?

Он давно знакомый мой, каждый угол в нем прямой,

Все четыре стороны одинаковой длины.

Вам его представить рад. Как зовут его? (…)

Колесо катилось. Вдруг ему навстречу вышел Круг:

«Ты, видать, моя родня, тоже круглый, как и я.

Сколько пальцем не веди, без углов выходим мы!

По дороге далеко нам катиться так легко!»

Тут навстречу им квадрат: «До чего ж друзьям я рад!

Покатился бы я с вами, да углы всегда мешали,

Их четыре у меня угловатых паренька,

Да четыре стороны все прямые, вот они.

И равны между собой, полюбуйся-ка любой!

Ну-ка пальцем проведи: есть преграды на пути.

Мне катиться не дано, зато ждет меня окно.

Нам дружить приятно, по всякому квадратно!»

III этап – 3-4 года

Цель: познакомить с треугольником, выделяя его характерные особенности; продолжать учить сравнивать известные геометрические фигуры между собой.

Используются те же приемы работы. Необходимо учесть, что треугольник дети сравнивают и с кругом, и с квадратом, находя все признаки сходства и отличия. Кроме того, фигуры необходимо демонстрировать в разном пространственном положении для подведения к обобщению. Для закрепления предлагаются задания на сериацию, группировку, выкладывание узоров, мозаика.

IV этап – 4-5 лет

Цель: познакомить с прямоугольником, учить называть и различать круг, квадрат, треугольник и прямоугольник; дать представление о характерных признаках этих фигур (наличие углов, сторон, их количество, соотнесение по размеру).

При знакомстве с прямоугольником необходимо помнить, что для различения этой фигуры ребенок должен владеть элементарным обобщением, т.к. квадрат то же является прямоугольником.

Подбирая наглядный материал, учесть, что у прямоугольника длина должна быть в два раза больше ширины (на первых занятиях), длины сторон квадрата должны быть равны ширине прямоугольника. Это используется для выявления особенностей этих фигур.

Постепенно от сравнения практическим путем переходить к сравнению на глаз.

Сравнивая прямоугольник с другими фигурами, уточнить представления детей о квадрате и треугольнике: у них разное количество углов, побуждать детей к счету углов, сторон.

Фигуры для сравнения предлагаются разного цвета, величины, изменяется соотношение сторон, чтобы создать предпосылки для обобщения на основе выделения существенных свойств – «все квадраты».

Фрагмент занятия: Незнайка приносит детям посылку и говорит:

- Сейчас мы будем играть: я буду доставать фигуры, а вы будете их отгадывать. (Достает круг).

- Что это? А как догадались?

- А теперь я отгадаю. (Достает треугольник). Это квадрат. Почему нет? А что это?

- А как эта фигура называется? (Достает квадрат).

- Ой, а этой фигуры я не знаю. (Достает прямоугольник). Может, это тоже квадрат?

Воспитатель:

- Нет, Незнайка, это не квадрат, хотя и очень похож на него. Это его старший брат – прямоугольник. Давайте на него внимательно посмотрим (выставить все фигуры перед детьми).

- У прямоугольника есть стороны (показать), углы (показать веером) и вершины (показать точкой); предложить то же самое сделать детям. Затем найти эти части у квадрата и треугольника. Так же дети работают с раздаточным материалом.

- Чем похож прямоугольник на квадрат? А на треугольник? Давайте их сосчитаем: сколько сторон? Углов? Вершин? У какой фигуры тоже 4 стороны, 4 угла и 4 вершины? Почему их можно назвать «братьями»?

- Чем отличается прямоугольник от квадрата? Давайте их приложим друг к другу. Что вы видите? (далее с помощью прикладывания, перегибания, использования эквивалента обобщить, что у квадрата все стороны равны, а у прямоугольника только по две равные стороны).

V этап – 5-6 лет

Цель: познакомить с четырехугольником, дать общее представление о том, что у любого четырехугольника по четыре стороны, угла и вершины.

Фрагмент занятия: на фланелеграфе выставляется набор геометрических фигур разного цвета и размера:

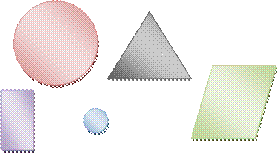Вопросы для анализа:

· На какие группы можно разделить все фигуры? (с углами и без)

· Какая из оставшихся фигур лишняя и почему? (треугольник)

· Названия каких из оставшихся фигур вы знаете? (квадрат, прямоугольник)

· А как могут называться эти фигуры? Давайте придумаем вместе.

· Чем похожи все эти фигуры? (у них по 4 угла…)

· Почему треугольник так называется?

· Если у этих фигур по 4 угла, то, как их можно назвать?

· Покажите теперь все четырехугольники.

· Можно ли квадрат и прямоугольник назвать четырехугольниками? Почему?

В старшей группе для правильных обобщений геометрические фигуры необходимо демонстрировать в разных положениях с варьированием несущественных признаков. При этом дети должны уметь выделить части фигур, сравнить их по свойствам.

VI этап – 5-6 лет

Цель: дать общее представление о многоугольнике, овале; учить различать границы многоугольника, внутреннюю и внешнюю области фигуры; познакомить с геометрическими телами: шар, куб, цилиндр, конус.

Эта задача решается на основе рассматривания геометрических фигур, анализа их строения, выделения существенных признаков. Понятие «многоугольник» вводится на основе обобщения: все фигуры, имеющие углы, называются многоугольниками.

Можно подойти к понятию «многоугольник» через понятие «точка». Для этого рассмотреть с детьми, как из точек путём их очень близкого расположения друг с другом получаются линии, которые могут быть кривыми (показать на модели провисшей ниточки), прямыми (нитку натянуть), найти эти линии в окружающей обстановке. Далее продемонстрировать, как получается отрезок (вырезать часть нитки), показать, что его можно нарисовать, что палочка – это тоже модель отрезка. Затем несколько отрезков (палочек) прикладываются друг к другу таким образом, что конец одного отрезка служит началом другого – так получается ломаная линия.

Теперь можно сравнить ломаную незамкнутую и ломаную замкнутую линии, уточнить, на что похожа замкнутая ломаная линия – это и есть многоугольник.

Многоугольники бывают разные : треугольник, четырехугольник, квадрат и т.д.. Провести упражнение «Разговор фигур» (по аналогии с упражнением «Разговор чисел»): «У меня больше углов», «А у меня меньше углов)» (цветными стрелками).

Презентация «Упражнения на геометрические преобразования»

· С помощью штриховки и обведения выделить области фигуры и ее границу.

· Определить характер взаимного расположения геометрических фигур на плоскости: какие фигуры находятся вне круга? внутри квадрата? за границей фигуры? справа? и т.п.

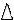· Какие фигуры могут получиться при пересечении квадрата и треугольника? Прямоугольника и четырёхугольника? и др. Сначала анализ выполнить на «прозрачных моделях», затем по представлению.

· Начерти фигуры так, чтобы областью пересечения был треугольник; чтобы круг был частью квадрата; чтобы фигуры не имели общих точек и т.п.

В старшей и подготовительной группах одно из направлений работы – преобразование разных геометрических фигур двумя способами: разрезанием и складыванием. Данная работа в целом проводится уже со средней группы не только в процессе специальных занятий. Дети в играх с мозаикой осваивают принципы получения новых геометрических фигур путем складывания. Однако в этом случае знания детей носят стихийный характер и мало связаны с формированием геометрических представлений. В старшем возрасте данный вид работы приобретает особую значимость, поэтому упражнения необходимо предлагать в системе.

Сначала необходимо уточнить и дополнить знания детей о способах получения новых фигур путем разрезания. Эта работа проводится в тесной связи с изучением отношений между частью и целым. Предлагаются следующие типы заданий:

· деление геометрических фигур на части указанной формы (перегибание, разрезание, линиями)

С этой целью можно прочитать стихотворение:

Давным-давно в темном лесу в фигурной избушке жили-были два брата, два квадрата. И были они близнецами. Убедитесь сами:

Видите на картинке – у каждого 4 стороны, 4 угла и 4 вершинки.

Гулял как-то первый квадрат между кустами, стучал по дорожке четырьмя уголками. А звери говорят: «Кто это? Первый квадрат или его брат, второй квадрат? Как же они похожи!

Помните на картинке: 4 стороны, 4 угла и 4 вершинки.

Надоело квадрату, что его путают с братом, и решил он измениться, в другую фигуру превратиться.

Взял он ножницы и срезал себе четыре уголка. В круг превратился и по дорожке покатился.

И живется теперь братьям чудно, перепутать теперь братьев трудно:

Один катается по дорожкам, другой ходит на четырех уголках - четырех ножках. До сих пор дружат два брата – круг с квадратом.

· составление фигур из имеющихся по заданным условиям: из 2-х треугольников – квадрат, из 2-х квадратов – прямоугольник, из 2-х треугольников – треугольник и т.п.… Целесообразно предлагать самостоятельно определять, какие фигуры могут получиться из данного набора фигур.

Для закрепления, систематизации знаний, развития устойчивых представлений о геометрических фигурах и их свойствах, для развития геометрического и пространственного мышления необходимо: лепить геометрические фигуры; выкладывать их из палочек; конструировать из проволоки; вырезать из бумаги; чертить, рисовать от руки и т.д.

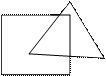
· распознавание геометрических фигур на чертеже:

- найти три треугольника и три четырехугольника

- сколько всего треугольников?

- сколько здесь фигур и какие?