Энтропия

Величина 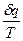при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния. Она называется энтропия. Эта функция возникла в ходе теоретического поиска наиболее благоприятных условий превращения теплоты в работу в тепловых двигателях.

Энтропия обозначается для 1 кг газа через s и измеряется в 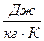. Для произвольного количества газа энтропия, обозначаемая через S, равна 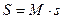и измеряется в .

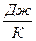Таким образом, аналитически энтропия определяется следующим образом:

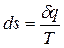(1.12).

Формула справедлива для реальных и идеальных газов.

Подобно любой другой функции состояния энтропия может быть представлена в виде функции любых двух параметров состояния:

; ; .

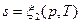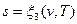Значение энтропии для заданного состояния определяется интегрированием уравнения (1):

,

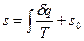где s₀ – константа интегрирования.

Тепловая теорема Нернста: при температуре, стремящейся к абсолютному нулю, энтропия вещества, находящегося в конденсированном состоянии с упорядоченной кристаллической структурой, стремится к нулю, т.е. s₀=0 при Т=0 К. Данный закон позволяет рассчитать абсолютное значение энтропии в отличие от внутренней энергии или энтальпии, которые всегда отсчитываются от произвольного уровня.

В технической термодинамике обычно используют изменение энтропии в каком либо процессе, поэтому энтропию тоже часто отсчитывают от произвольно выбранного уровня:

.

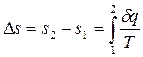Понятие энтропии позволяет ввести чрезвычайно удобную для термодинамических расчетов T,s – диаграмму, на которой (как и на p,v –диаграмме) состояние термодинамической системы изображается точкой, а равновесный термодинамический процесс линией.

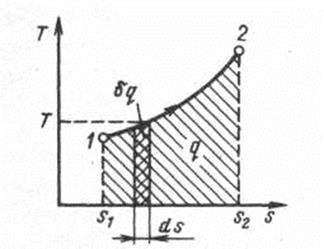
Рис. 1.6. Графическое изображение теплоты в

T,s – координатах

В равновесном процессе

,

.

В T,s – диаграмме элементарная теплота процесса δq изображается элементарной площадкой с высотой Т и основанием ds, а площадь, ограниченная линией процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса. При подводе теплоты к телу (δq>0)его энтропия возрастает (δs>0), а при отводе (δq<0)его энтропия убывает (δs<0).