Оптическое свойство эллипса

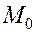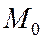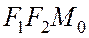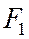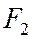Теорема: Касательная к эллипсу в произвольной его точке является биссектрисой внешнего угла треугольника , имеющего своими вершинами фокусы и эллипса и данную точку .

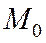Доказательство. Рассмотрим уравнение касательной к эллипсу 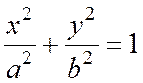в данной на нем точке :

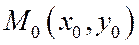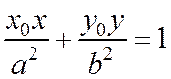
Отношение расстояни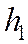й и 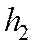от фокусов 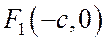и 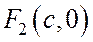эллипса до касательной в точке 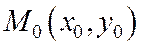равно отношению модулей результатов подстановки координат фокусов 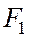и 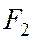в левую часть уравнения касательной.

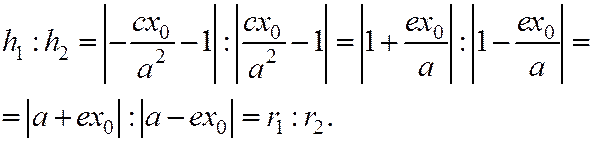
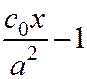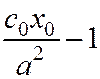Отметим, что результаты подстановок – и координат фокусов 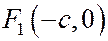и 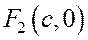в левую часть уравнения касательной – числа одного знака:

;

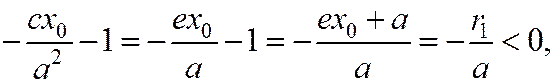
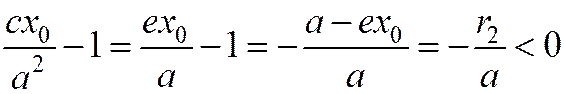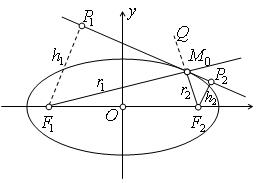
поэтому оба фокуса 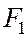и расположены по одну сторону от касательной к эллипсу в произвольной его точке.

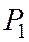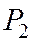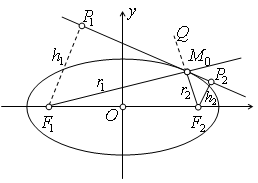
Обозначить через и основания перпендикуляров, опущенных из фокусов эллипса на касательную к нему, проведенную в точке 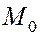(рис.).

Тогда 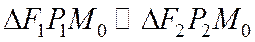, так как они прямоугольные и по доказанному

,

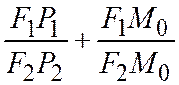поэтому 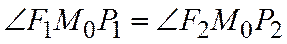, следовательно, угол 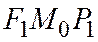равен углу 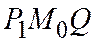, где точка 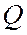лежит на продолжении отрезка 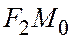за точку .

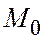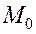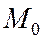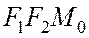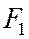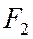Поэтому касательная к эллипсу в произвольной его точке является биссектрисой внешнего угла треугольника , имеющего своими вершинами фокусы и эллипса и данную точку 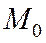. Теорема доказана.

Из этой теоремы непосредственно вытекает способ построения касательной к эллипсу в произвольной его точке.

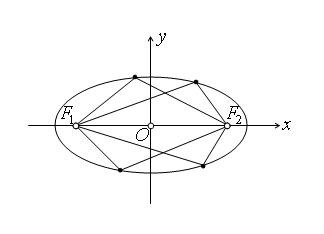
Доказанной теореме можно дать следующую физическую интерпретацию: если поместить в один из фокусов эллипса источник света, то лучи после отражения их от эллипса соберутся в другом фокусе, так как световой луч отражается от эллипса, как от касательной, проведенной к эллипсу, в точке падения луча (см. рис.). Слово фокус по латыни означает «очаг».

Дома. Параграф 18 по Клетенику. №444-№454