Параметрические уравнения эллипса
Пусть дан эллипс каноническим уравнением 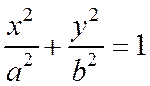 . (1)
. (1)
Рассмотрим окружность
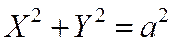 , (2)
, (2)
которая переходит в данный эллипс в результате сжатия
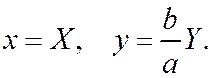 (3)
(3)
Пусть М(х, у) – произвольная точка данного эллипса, 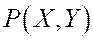 - ее образ на окружности. Обозначим через
- ее образ на окружности. Обозначим через 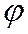 угол от положительного направления оси Ох до луча ОР.
угол от положительного направления оси Ох до луча ОР.
Тогда
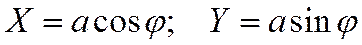
и, следовательно,
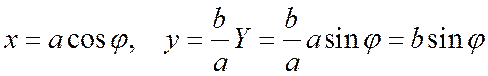 .
.
 Уравнения
Уравнения

И являются параметрическими уравнениями эллипса.
Параметр 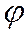 называется эксцентрическим углом точки эллипса. Если задана точка
называется эксцентрическим углом точки эллипса. Если задана точка 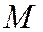 эллипса, то для нахождения
эллипса, то для нахождения 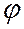 надо построить окружность на большей оси эллипса как на диаметре и через точку М провести прямую, параллельную малой оси эллипса.
надо построить окружность на большей оси эллипса как на диаметре и через точку М провести прямую, параллельную малой оси эллипса.
Точка 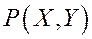 пересечения этой прямой с окружностью, лежащая по ту же сторону от большей оси эллипса, что и точка М, является прообразом точки М(х,у) при равномерном сжатии
пересечения этой прямой с окружностью, лежащая по ту же сторону от большей оси эллипса, что и точка М, является прообразом точки М(х,у) при равномерном сжатии 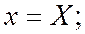
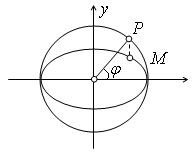
 Угол от оси Ох до луча ОР и являются эксцентрическим углом
Угол от оси Ох до луча ОР и являются эксцентрическим углом 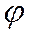 , соответствующим взятой точки М на эллипсе (см. рис.).
, соответствующим взятой точки М на эллипсе (см. рис.).
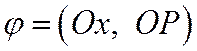
Дата добавления: 2015-08-11; просмотров: 920;
