Бесконечная балка на упругом основании
Этой моделью можно описать, например, поведение дорожного полотна с автомобилем веса Р. Погонная сила 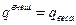 представляет собой погонный вес полотна. Мы можем представить общее решение как сумму решения 2-х задач: задачи о действии только силы веса qвеса и задачи о действии только силы Р. Здесь
представляет собой погонный вес полотна. Мы можем представить общее решение как сумму решения 2-х задач: задачи о действии только силы веса qвеса и задачи о действии только силы Р. Здесь 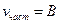 соответствует случаю когда, действует лишь qвеса.
соответствует случаю когда, действует лишь qвеса.
Прогиб 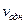 , который содержит,
, который содержит, 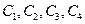 , соответствует случаю
, соответствует случаю 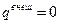 ,
, 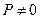 . Рассмотрим этот случай.
. Рассмотрим этот случай.
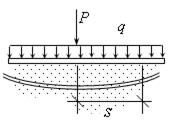
рис.16.17
Пусть s – расстояние от силы Р до сечения.
Слева и справа прогиб симметричный, поэтому исследуем прогиб v только справа, то есть, найдем функцию v(s).
Для отыскания 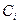 учтем, что прогиб должен быть ограничен при любых s. Однако первые 2 слагаемых не ограничены, т.е.
учтем, что прогиб должен быть ограничен при любых s. Однако первые 2 слагаемых не ограничены, т.е.
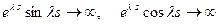 при
при 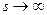 .
.
Отсюда вытекает, что должно быть 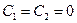 .
.
Хотя для анализа решения можно и не искать С3, С4, найдем их для иллюстрации того как находится выражение для прогиба.
В силу симметричности задачи под силой должно быть
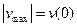 .
.
По теореме Ферма имеем соотношение:
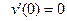 .
.
Подставляя получаем:
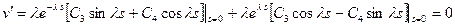 (16.23)
(16.23)
Отсюда:
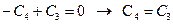
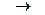
 (16.24)
(16.24)
Следующее уравнение относительно 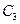 получим из статических соображений. Виду симметричности задачи реакция основания справа (см. рис 16.18) известна:
получим из статических соображений. Виду симметричности задачи реакция основания справа (см. рис 16.18) известна: 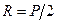 .
.
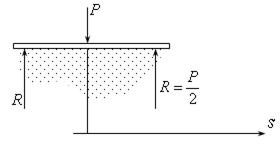
рис.16.18
Как видно из рис.16.18 в сечении под силой (при s = 0) согласно определению поперечной силы
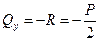 . (16.24)
. (16.24)
Из уравнения (16.18) получим:
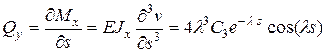 . (16.25)
. (16.25)
Подставляя s = 0 находим из (16.24):
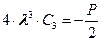 .
.
Отсюда: 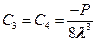 .
.
Итак: 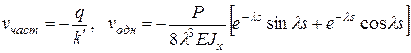 .
.
Дата добавления: 2015-08-11; просмотров: 837;
