Граничные условия для касательных составляющих векторов поля

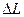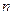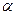Найдем граничные условия для касательных составляющих векторов напряженностей поля. Для этого сначала применим интегральную форму первого уравнения Максвелла к контуру (рис. 2б). Пусть и — орты нормали и касательной к поверхности S в точке 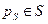(предполагаем, что нормаль и касательная в каждой точке 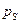существуют). Введем в точке 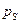орт 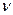такой, что 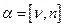. Считаем, что на контур 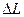натянута поверхность 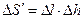и .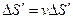

При 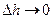имеем: .

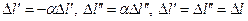Интеграл по замкнутому контуру 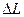представляется в виде суммы интегралов по частям контура 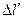, 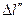и двух интегралов по боковым сторонам 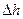. Но если 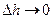, то два последних интеграла стремятся к нулю. В интеграле правой части равенства при малом 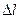можно воспользоваться теоремой о среднем и вынести плотность полного тока из-под знака интеграла. Таким образом, получаем

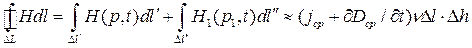(8)

Применим к контуру 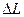второе уравнение Максвелла в интегральной форме с учетом заданной плотности стороннего магнитного тока

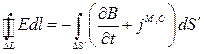, где 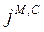- фиктивные сторонние токи

При 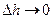при тех же условиях, получаем

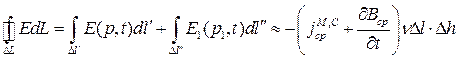(9)

В реальных средах на поверхности раздела 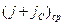и 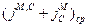не обращаются в бесконечность (не имеют особенности), поэтому их произведения на 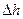при 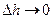стремятся к нулю. Применяя теорему о среднем и сокращая результат на 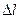, имеем

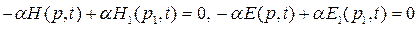
Если 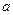— некоторый вектор, то 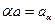— определяет касательную к поверхности S составляющую этого вектора. Таким образом, последние равенства дают математическую запись граничных условий на поверхности раздела сред

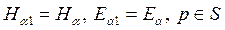(10)

т.е. касательные составляющие векторов напряженностей электрического и магнитного полей остаются непрерывными при переходе через поверхность раздела реальных сред. Для комплексных амплитуд получаем:

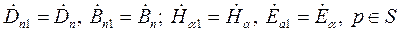(11)