Граничные условия на поверхностях раздела реальных сред
Тема 3
Неоднородная среда в общем случае имеет диэлектрическую и магнитную проницаемости и проводимость, являющиеся функциями координат. Но на поверхности раздела двух разных сред эти функции испытывают разрыв (скачок). Например, на поверхности раздела металл-воздух проводимость и диэлектрическая проницаемость меняются скачком. Уравнения Максвелла в дифференциальной форме описывают ЭМ поле в обыкновенной точке пространства, поэтому на поверхности раздела сред, где нарушается непрерывность параметров среды, они теряют смысл и должны быть дополнены условиями, определяющими поведение векторов поля в точках скачка параметров сред. Эти условия устанавливаются с помощью уравнений Максвелла в интегральной форме.
Пусть некоторый объем V заполнен веществом с параметрами 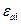 ,
, 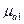 ,
, 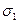 и ограничен поверхностью S (рис. 2).
и ограничен поверхностью S (рис. 2).
а б
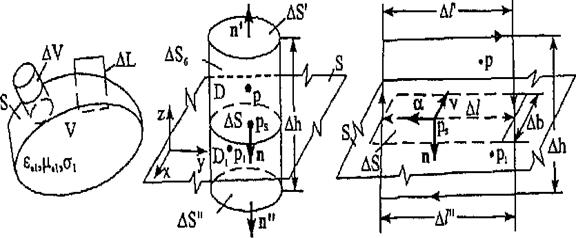
Рис.2 К выводу граничных условий
Векторы ЭМ поля внутри тела обозначим через 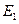 ,
, 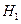 ,
, 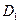 ,
, 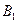 . Тело находится в среде с параметрами
. Тело находится в среде с параметрами 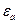 ,
, 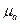 ,
, 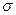 . Векторы поля в среде обозначим через
. Векторы поля в среде обозначим через  ,
, 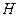 ,
, 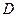 ,
, 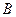 . Поверхность S есть поверхность раздела сред.
. Поверхность S есть поверхность раздела сред.
Выделим у поверхности S некоторый элементарный объем 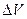 цилиндрической формы с длиной образующей
цилиндрической формы с длиной образующей 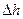 и контур
и контур 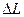 с длиной боковой стороны
с длиной боковой стороны 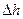 , такие, что часть
, такие, что часть 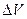 и часть
и часть 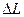 находятся в среде, а другие их части — в объеме V. Считаем, что
находятся в среде, а другие их части — в объеме V. Считаем, что 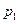 и
и 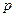 — точки наблюдения ЭМ поля расположены соответственно в объеме
— точки наблюдения ЭМ поля расположены соответственно в объеме 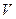 и в среде. Тогда с помощью уравнений Максвелла в интегральной форме можно связать векторы поля в точках
и в среде. Тогда с помощью уравнений Максвелла в интегральной форме можно связать векторы поля в точках 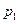 и в точках
и в точках 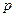 . Если затем положить
. Если затем положить 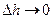 , то точки
, то точки 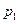 и
и 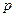 стремятся на поверхность S раздела сред, т.е.
стремятся на поверхность S раздела сред, т.е. 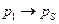 и
и 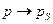 , где
, где 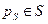 .
.
Дата добавления: 2015-08-11; просмотров: 916;
