Элементы геометрической оптики.

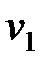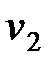Пусть волна падает на границу раздела двух сред. Скорость волны в рассматриваемых средах соответственно равны и . На границе раздела сред волна частично отражается, а частично переходит во вторую среду (рис. 1).

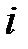ФРОНТ ОТРАЖЕННОЙ ФРОНТ ПАДАЮЩЕЙ 1 ВОЛНЫ 2 ВОЛНЫ D B  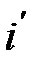 A C   ФРОНТ ПРЕЛОМЛЕННОЙ ВОЛНЫ E r

Рис. 1

Для нахождения законов отражения и преломления волн воспользуемся принципос Гюйгенса, согласно которому каждая точка среды, до которой доходит волна, становится источником вторичных волн, огибающая которых формирует положение нового фронта волны. Поэтому, когда волна (рис.1) дойдет до т.А (луч 1), то от нее, как от вторичного источника, начнет распространяться сферическая волна: в первой (верхней среде) со скоростью v₁, во второй (нижней среде) v₂.

Через промежуток времени 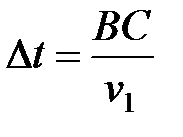, когда до границы раздела дойдет вторая волна (луч 2), радиусы сферических поверхностей в 1-й и 2-й средах станут равными

; .

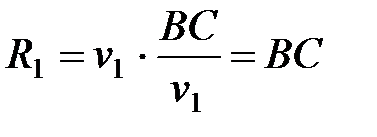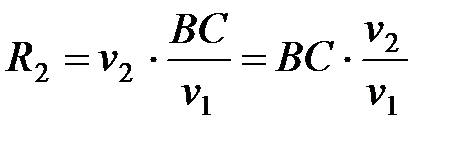Положения фронтов отраженной и преломленной волн определятся касательными плоскостями к сферическим волнам, исходящим из т.А в первую и вторую среды. Тогда следует:

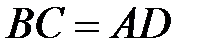и .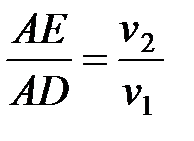

Из геометрических построений следуют выводы.

Закон отражения: отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения; угол 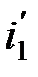отражения равен углу 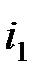падения:

.

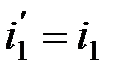Закон преломления: луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред:

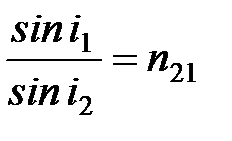, (1)

где n₂₁ – относительный показатель преломления второй среды относительно первой. Индексы в обозначении углов указывают, в какой среде (первой или второй) идет луч. Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления:

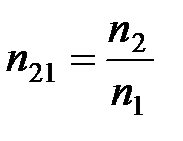. (2)

Абсолютным показателем преломления среды называется величина п, которая равняется отношению скорости с электромагнитных волн в вакууме к их фазовой скорости v в среде:

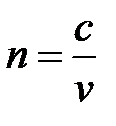. (3)

Учитывая, что фазовая скорость в среде определяется выражением

,

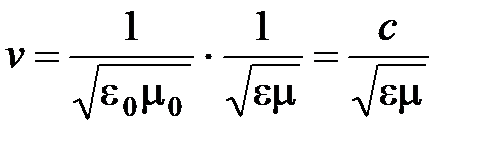следует, что 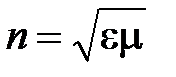. Поэтому закон преломления можно записать в виде

. (4)

Из симметрии (4) вытекает обратимость световых лучей. Если обратить луч III (рис.1), заставив его падать на границу раздела под углом i₂, то преломленный луч в первой среде будет распространяться под углом i₁, т.е. пойдет в обратном направлении вдоль луча I.

Предельный угол падения. При переходе волны из среды с большим показателем преломления в среду с меньшим показателем преломления 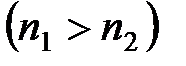угол падения i будет меньше угла преломления r (рис.2а).

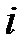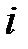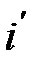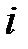а) б) в)     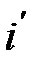r r

Рис. 2а,б,в

С увеличением угла падения i = i_пр можно получить угол преломления 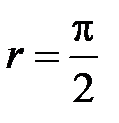, т.е. преломленный луч будет скользить по поверхности раздела этих сред. Угол удовлетворяющий условию:

, при котором 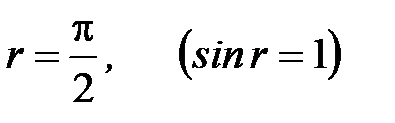(5)

называется предельным углом преломления луча.

При (рис.2а,б) падающий луч частично отражается, частично переходит во вторую среду после преломления. При условии 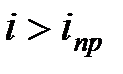(рис.2в) луч не преломляется, а полностью отражается обратно в первую среду. Это оптическое явление называется полным внутренним отражением.