Процессы под нагрузкой

При нагружении вала 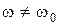; отличие скоростей w и w₀ принято характеризовать скольжением

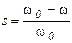. (4.5)

Теперь в роторной цепи появится ЭДС 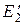, наведенная по закону электромагнитной индукции и равная

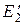=E_1¢s; (4.6)

штрихом здесь и далее отмечены приведенные величины, учитывающие неодинаковость обмоток статора и ротора. Частота наведенной ЭДС составляет

f₂=f₁s (4.7)

Ток I₂^¢ в роторной цепи, обладающей сопротивлением R₂^¢ и индуктивностью L₂^¢, определится как

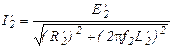
или после простых преобразований

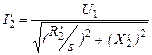, (4.8)

где Х₂^¢ - индуктивное сопротивление рассеяния вторичной цепи при частоте f₁.

Мы получили уравнение, соответствующее традиционной схеме замещения фазы асинхронного двигателя - рис. 4.3, в которой учтены и параметры статора R₁ и Х₁. Эта простая модель пригодна для анализа установившихся режимов при симметричном двигателе с симметричным питанием.

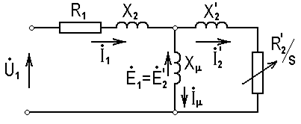
Рис. 4.3. Схема замещения фазы асинхронного двигателя

Для получения механической характеристики ещё более упростим модель - вынесем контур намагничивания на зажимы - рис. 4.4,а, как это часто делается в курсе электрических машин.

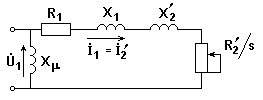
а) б)

Рис. 4.4. Упрощенная схема замещения (а) и характеристики асинхронной машины (б)

Поскольку

,

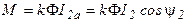где I_2а - активная составляющая тока ротора,

y₂ - угол между 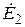и ,

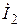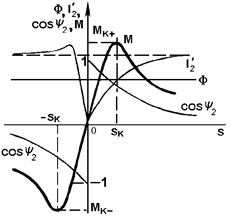
качественное представление о механической характеристике М(s) можно получить, проследив зависимость каждого из трех сомножителей от s.

Магнитный поток Ф в первом приближении в соответствии с (4.4) не зависит от s - рис. 4.4,б. Ток ротора (4.8) равен нулю при s = 0 и асимптотически стремится к 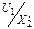при s ® ±¥ - рис. 4.4,б. Последний сомножитель легко определить по схеме замещения:

;

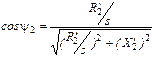cosy₂ близок к ±1 при малых s и асимптотически стремится к нулю при s ® ±¥. Момент, как произведение трех сомножителей, равен нулю при s = 0 (w = w₀ - идеальный холостой ход), достигает положительного М_к+ и отрицательного М_к- максимумов - критических значений при некоторых критических значениях скольжения 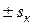, а затем при s ® ±¥ стремится к нулю за счет третьего сомножителя.

Уравнение механической характеристики получим, приравняв потери в роторной цепи, выраженные через механические и через электрические величины. Мощность, потребляемая из сети, если пренебречь потерями в R₁, примерно равна электромагнитной мощности:

,

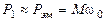а мощность на валу определяется как

.

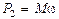Потери в роторной цепи составят

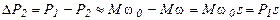(4.9)

или при выражении их через электрические величины

,

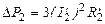откуда

.

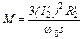Подставив в последнее выражение I₂^¢ из (4.8) и найдя экстремум функции М=f(s) и соответствующие ему М_к и s_к, будем иметь:

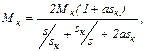(4.10)

где а=R₁/R¢₂: