Лекция 13. Преобразование К.Ч. вращением вокруг прямой уровня.

Преобразование К.Ч. вращением вокруг прямой уровня.

В процессе преобразования повернем плоскость треугольника АВС, заданную на К.Ч. (Рис.60) двумя проекциями (А₁ В₁ С₁, А₂ В₂ С₂) вокруг прямой уровня (горизонтали) h (h₁, h₂) до совмещения с горизонтальной плоскостью уровня L (L₂), проходящей через ось вращения h. Для упрощения построений горизонталь h (ось вращения) проведем через точку С (при повороте точка С будет неподвижной). Точка А, вращаясь вокруг оси h, опишет окружность, плоскость которой, как известно, перпендикулярна оси вращения. Данная окружность на основании теоремы о проецировании прямого угла спроецируется на горизонтальную плоскость проекций П₁ в виде прямой перпендикулярной проекции h₁ оси вращения h. На этой прямой от точки О₁ откладываем натуральную величину (О₁ А*) радиуса вращения точки А, которую предварительно определим с помощью прямоугольного треугольника О₁ А₁ А*.

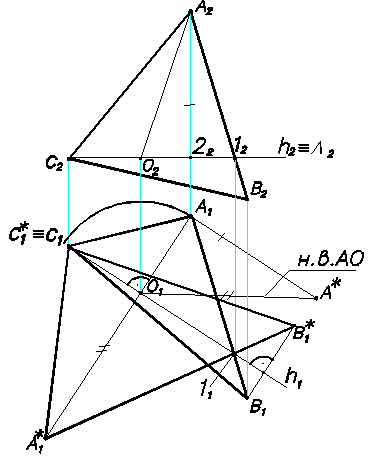Таким способом мы определим положение проекции А₁* точки А после поворота. Проекцию В₁* точки В после поворота можно построить без определения радиуса ее вращения.

Для этого используем неподвижную точку 1_1. Дальнейшие построения не представляют особой сложности (см. Рис.60). Полученная на П₁ при вращении вокруг линии уровня h₁ проекция (А₁* В₁* С₁*) плоскости треугольника АВС принадлежит плоскости уровня L (L₂) и является натуральной величиной треугольника АВС.

Рис.60