Модели оценки надежности программных средств
Известны десятки МНПС, разработанные в 1970-2006 гг.. Однако, сейчас ситуация такова, что каждая фирма-разработчик ПС или иная организация, заинтересованная в количественной оценке надежности ПС, вынуждены решать проблему для себя заново, учитывая опыт и квалификацию программистов и проектировщиков, специфику создаваемых систем, требования к их надежности и безопасности, экономические аспекты и др.. Необходимость решения данной задачи связанна с узкой специализацией большинства существующих моделей и с трудностью выбора одной из них для конкретных ПС.
Подход, основанный на стремлении разработать модель оценки надежности для очередного проекта или даже группы проектов, является в некотором смысле экстенсивным. Альтернативный подход может базироваться на систематизации множества известных моделей, выборе и последующей настройке их параметров.
Под надежностью функционирования ПС, как одним из свойств, определяющих качество ПС, понимается группа свойств, обусловливающая способность ПС сохранять работоспособность и преобразовывать исходные данные в искомый результат в заданных условиях за установленный период времени. Однако, следует помнить, что ПС не подвержены износу или старению. Количество и характер отказов, связанных с ПС, является следствием его внутренних дефектов (дефектов проектирования) и зависит от условий его применения. При этом отказом называется событие, заключающееся в проявлении неработоспособности ПС, а ошибкой - запись элемента программы или программной документации, использование которой приводит (или может привести) к непредвиденной ситуации.
Классификация МНПC дана в [1], где с точки зрения методической основы их построения данные модели подразделяются на эмпирические, статистические и вероятностные.
Проанализируем данные классы МНПС с точки зрения целесообразности применения их при решении задачи комплексной оценки надежности СВГ с учетом дефектов программно-аппаратных средств.
Эмпирические модели для оценки надежности ПС являются наиболее простыми. Они основаны на анализе накопленной информации о функционировании ранее разработанных программ.
Модель Холстеда оценивает количество ошибок в программе после окончания ее разработки по формуле [1]:
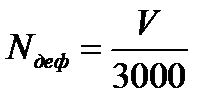 , (3.2)
, (3.2)
где V – объем программы,
Екрит – программное значение способности человеческого мозга, характеризующее его возможности обрабатывать пять "объектов". Это значение для английского языка составляет 3000.
Эмпирическая модель фирмы IBM [1] оценивает число дефектов в различных редакциях операционной системы:
Ni = ИЗМі = α×МИМі + γ×ИМі , (3.3)
где ИЗМі – общее число изменений, вносимых в программные модули;
і – порядковый номер обновления;
ИМі – количество исправляемых модулей (меньше 10 исправлений);
МИМі – количество многократно исправляемых модулей (более 10 исправлений);
ИМі = 0,9×НМі + 0,15×СИМі ; (3.4)
МИМі = 0,15×ИМі + 0,06×СИМі ; (3.5)
где НМі – количество новых модулей;
СИМі – количество старых исправляемых модулей.
Коэффициенты α и γ показывают среднее количество изменений вносимых на один модуль в соответствующих группах ИМ и МИМ (по умолчанию α = 23, γ = 2).
Однако эмпирические модели грубы. Расхождения между оценками Nош и фактическими результатами могут быть большими. Несмотря на это, на этапе разработки программ эти модели получили широкое применение. Причем наиболее употребительной стала модель Холстеда, ввиду ее простоты [1].
В статистических моделях оценка надежности ПС связана с числом программных дефектов пропорциональными соотношениями.
В модели Г.Милса [1] в рассматриваемое ПС случайным образом вносится некоторое количество известных дефектов и предполагается, что темп обнаружения собственных дефектов в программе и внесенных одинаков. Тогда число собственных дефектов выражается соотношением:
 , (3.6)
, (3.6)
где Nош 1 и Nвнош 1 – число выявленных собственных и внесенных дефектов. При этом предполагается, что число Nош 1 не превышает прогнозируемого числа дефектов до начала тестирования, определенного метриками М. Холстеда, а все внесенные дефекты выявлены и устранены.
Существенным недостатком эмпирических и статистических моделей является то, что они не учитывают динамику реального вычислительного процесса [2] и не позволяют оценить надежность ПС СВГ, используемых по назначению с учетом времени и условий функционирования. Однако оценка надежности ПС с учетом времени функционирования важна при определении комплексного показателя надежности – коэффициента готовности СиТВГ с учетом отказов АС и ПС. Получить такую оценку позволяют вероятностные модели, которые являются наиболее представительной группой моделей надежности ПС [1]. Среди них можно выделить графовероятностные, вероятностно-лингвистические и экспоненциальные модели.
Графовероятностные модели базируются на анализе всех (или подмножества) путей в графах-схемах программ G и оценки вероятности их безошибочного выполнения Pп(G) с учетом вероятностей возможных значений ветвления p(xi). Такие модели дают точные оценки надежности ПС, однако их применение затруднительно из-за большой размерности граф-схем, а также сложности получения значений вероятностей p(xi) и вероятностей безошибочного выполнения вершин графа G.
Вероятностно-лингвистические модели базируются на аппарате нечетких множеств. Они трактуют оценку показателя надежности, как нечеткое множество, каждому элементу которого ставится в соответствие значение функции принадлежности.
Известные экспоненциальные модели [2] базируются на следующих допущениях: интенсивность проявления дефектов проектирования пропорциональна их остаточному уровню в ПС; время до проявления очередного ДП распределено экспоненциально; каждый обнаруженный дефект устраняется немедленно, а новые дефекты не вносятся. Первое из этих допущений базируется на установленном Джелински и Морандой [5] факте того, что после каждого устранения дефекта интенсивность отказов скачком изменялась на постоянную величину, а в промежутках между устранениями дефектов оставалась постоянной. При этом, чтобы определить общее число дефектов в программном обеспечении и коэффициент пропорциональности, связывающий интенсивность отказов с числом неустраненных дефектов, производилась оценка по методу максимального правдоподобия [5]. Что касается второго допущения, то статистический анализ данных о программных дефектах по нескольким представительным наборам независимых проектов показал, что эти данные не могут быть описаны каким-либо общим законом распределения. Однако, предположение об экспоненциальном характере закона распределения времени до проявления ДП экспериментально подтверждено Дж. Мусой для ряда проектов [2]. Третье допущение можно считать вполне справедливым для объектов с совершенными средствами контроля и диагностирования и высококвалифицированным обслуживающим персоналом.
Тогда вероятность безотказного выполнения программ на i-м интервале времени может быть вычислена по формуле:
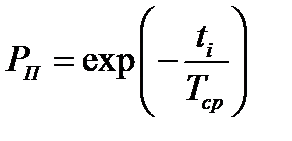 , (3.7)
, (3.7)
где Tср – средняя наработка на отказ, вычисляемая по формуле:
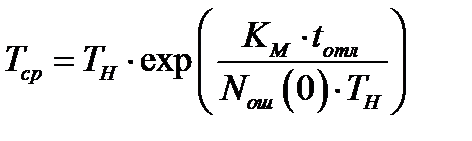 (3.8)
(3.8)
В свою очередь TН – средняя наработка на отказ в начале испытаний, tотл – длительность тестирования и отладки, KМ – коэффициент, который учитывает «уплотнение» времени тестирования и отладки по отношению к реальному времени функционирования СВГ.
Выражение для интенсивности проявления ДП ПС имеет вид
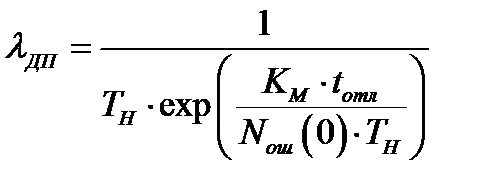 (3.9)
(3.9)
При этом параметр Nош(0) возможно определить с помощью модели Холстеда.
Как показывают исследования [6-8], на современном этапе применение методов повышения надежности АС позволяет получить систему с заданным уровнем надежности АС при приемлемых затратах. Однако высокая стоимость ПС не позволяет активно внедрять диверсные продукты в среднебюджетные системы. В то же время выявление и устранение программных дефектов на этапе тестирования также может позволить достичь заданного уровня надежности ПС, поэтому это направление остается перспективным. При этом необходимо решить задачу определения надежности ПС при устранении программных дефектов.
Модели безотказности ПС основаны на применении ряда метрик программы [9-13]. Двухуровневое представление ПС СВГ в виде взаимодействующих операционной системы (ОС) и прикладных программ предусматривает оценивание безотказности каждой из этих составляющих, что увеличивает размерность МН ПС. Поэтому далее рассматривается допущение об абсолютной надежности ОС, которое позволяет ограничиться рассмотрением МН прикладных программ.
На современном этапе для сложных ПС большого объема используют модели надежности, в которых рассматривается три класса неисправностей ПС :
- стабильные неисправности, вызванные т.н. «борбагами» (bohrbug), которые проявляются в строго определенных условиях и связаны с неполнотой тестирования и верификации ПС и устраняются при выполнении ремонтных операций;
- перемежающиеся неисправности, вызванные т.н. «гейзенбагами» (heisenbug) – дефектами ПС, которые исчезают или видоизменяются при попытке их выявления, и устраняются путем перезапуска ПС;
- неисправности, вызванные т.н. дефектами старения ПС (aging related bug), эти неисправности устраняются путем модернизации ПС.
Для рассматриваемого класса систем неисправности, вызванные «борбагами» и дефектами старения, некритичны, так как данные системы прошли качественную верификацию и тестирование ПС, а избыточность структуры СВГ позволяет проводить модернизацию ПС без нарушения работоспособного состояния системы в целом. Модели безотказности ПС с учетом проявления «гейзенбагов» редусматривают экспоненциальное распределение времени между отказами ПС.
Интенсивность отказов ПС может быть рассчитана на основе модели Мусы по формуле:
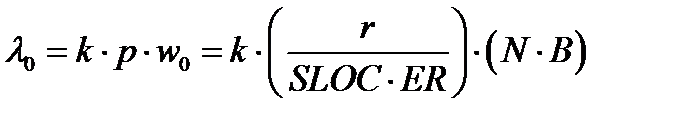 , (3.10)
, (3.10)
где k – постоянная, которая связана с динамическим строением программы и применением ПС на различных платформах АС, k 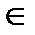 (1,4·10–7; 10,6·10–7), по умолчанию k = 4,2·10–7;
(1,4·10–7; 10,6·10–7), по умолчанию k = 4,2·10–7;
p – линейная частота обращения к программе;
w0 – количество строк программного кода, содержащих дефекты по умолчанию w0 = 6 (дефектов/1000 строк программного кода);
r – средняя частота обращений к командам программы, зависит от производительности процессора ЭВМ;
SLOC – количество строк исходного программного кода;
ER – коэффициент расширения кода, зависит от используемого языка программирования (для Assembler ER=1,0; для Macro Assembler, ER=1,5; для C ER=2,5; для Cobal, Fortran ER=3; для Ada ER=4,5);
N – количество дефектов ПС в тексте программы;
В – коэффициент проявления дефектов ПС, равен отношению количества дефектов, которые вызывают отказ СВГ к общему количеству дефектов ПС, невыявленных на этапе тестирования и верификации, по умолчанию В = 0,95.
Количество невыявленных дефектов ПС можно определить с помощью модели RL-92-52 [12] по формуле:
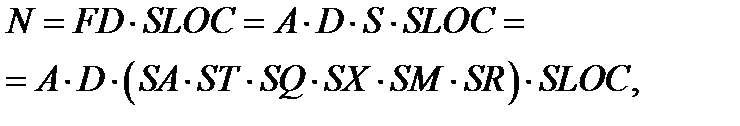 (3.11)
(3.11)
где FD – плотность дефектов (Fault density), отношение количества программных дефектов к количеству строк программного кода, содержащих эти дефекты (faults/SLOC);
A, D, S – коэффициенты, связанные с различными метриками ПС;
А (Application) – коэффициент, зависящий от сложности разработки различных типов приложений, А 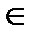 (2; 14) (дефектов ПС/тысяч строк программного кода);
(2; 14) (дефектов ПС/тысяч строк программного кода);
D (Development organization) – коэффициент, который характеризует методы разработки и инструментальные средства, D 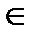 (0,5; 2);
(0,5; 2);
SA (Software anomaly management) – коэффициент, зависящий от применяемых методов отказоустойчивого проектирования, SA 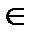 (0,9; 1,1);
(0,9; 1,1);
ST (Software traceability) – коэффициент, который характеризует возможность оперативного контроля проекта и кода ПС, ST 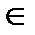 (0,9; 1);
(0,9; 1);
SQ (Software quality) – коэффициент, который характеризует наличие в ПС процедур контроля качества, SQ 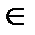 (1; 1,1);
(1; 1,1);
SX (Software complexity) – коэффициент, зависящий от сложности программных модулей, SX 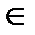 (0,8; 1,5);
(0,8; 1,5);
SM (Software modularity) – коэффициент, зависящий от объема программных модулей, SM 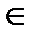 (0,9; 2);
(0,9; 2);
SR (Software standards review) – коэффициент, который характеризует наличие в ПС процедур поддержки различных стандартов, SR 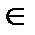 (0,75; 1,5).
(0,75; 1,5).
Как было отмечено, при моделировании функционирования ПС СВГ необходимо учитывать процессы обновления ПС. При обновлении ПС количество оставшихся дефектов после обновления ПС согласно модели IBM [1].
Для разработки моделей надежности СВГ, ориентированных на определение коэффициентов готовности и технического использования, необходимо обосновать подход к получению параметров, которые определяют надежность программной компоненты. Это параметры {λПС}i (интенсивность проявления ДП ПС i-го элемента СВГ) и {∆λПС}i (величина изменения {λПС}i i-го элемента СВГ после обновления ПС). Подход основан на комплексировании моделей надежности ПС Мусы, RL-92-52 и IBM. При этом учитывается допущение о том, что в процессе функционирования СВГ интенсивность отказов ПС элементов СВГ остается постоянной на промежутках между обновлениями ПС.
Предлагаемый метод определения параметров {λПС}i и {∆λПС}i, включает следующие этапы.
1. Расчет начальной интенсивности отказов ПС с помощью модели Мусы и плотности дефектов ПС с помощью модели RL-92-52. Согласно данных моделей начальная интенсивность отказов ПС определяется по формуле:
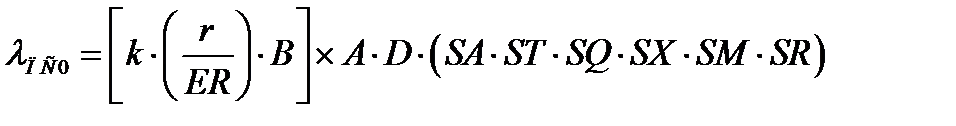 (3.12)
(3.12)
2. Оценивание параметра ∆λПС производится согласно модифицированной модели IBM. Количество дефектов после каждого обновления ПС определяется как:
Nj = 4,905 НМj + 4,105СИМj, (3.13)
где Nj – количество оставшихся дефектов ПС после j-го обновления ПС;
НМj – количество новых модулей;
СИМj – количество старых исправляемых модулей;
j – порядковый номер обновления ПС.
Изменение интенсивности отказов ПС определяется как:
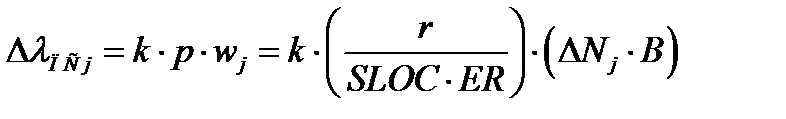 , (3.14)
, (3.14)
где ΔNj = Nj–1 – Nj – изменение количества ДП ПС после проведения j-го обновления программ.
3. Далее для оценивания надежности ПС СВГ используются показатели, аналогичные показателям надежности АС и базирующиеся на экспоненциальных вероятностных моделях.
Правомерность этого подхода обусловлена характером проявления ДП ПС (heisenbug).
Кроме того, при обновлении ПС устраняются причины отказов СВГ, вызванных злонамеренными действиями обслуживающего персонала и пользователей. При этом необходимо учитывать параметры ПС, которые определяют надежность СВГ с учетом ДВ ЗД. Это параметры {λЗД}i (интенсивность проявления ДВ ЗД i-го элемента СВГ) и {∆λЗД}i (величина изменения {λЗД}i i-го элемента СВГ после обновления ПС). При моделировании функционирования ПС с учетом ЗД принимаются следующие допущения:
- ДВ ЗД имеют критические последствия для работоспособности ПС СВГ (соответственно, необходимо выполнить выборку критических для готовности СВГ угроз из общего множества атак);
- восстановление системы после проявления ДВ ЗД производится путем перезапуска ПС и восстановления исходных данных для работы программ.
Интенсивность отказов ПС СВГ, вызванных ЗД, изменяется по закону:
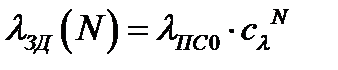 , (3.15)
, (3.15)
где λПС 0 – начальная интенсивность отказов СВГ, вызванныхЗД, которая определяется по формуле , так как в соответсвии с принятыми допущениями ДП ПС и ДВ ЗД имеют сходные первопричины появления и разные причины проявления;
сλ – скорость изменения интенсивности отказов;
N – порядковый номер отказа СВГ, вызванного злонамеренными действиями обслуживающего персонала и пользователей.
Скорость изменения интенсивности отказов определяется по закону:
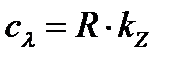 (3.16)
(3.16)
где коэффициент R показывает, что злоумышленник, который обнаружил «дыру» в ПС, либо поделится информацией с R другими злоумышленниками, либо в следующий раз будет тратить в R раз меньше времени на перевод системы в неработоспособное состояние (по умолчанию R = 2).
kz – коэффициент информационной безопасности (security) СВГ, который определяется исходя из класса СВГ в соответствии с таблицей 3.1:
Таблица 3.1 – Значения коэффициента
безопасности (security)
| Класс безопасности | kz |
| 0,95 | |
| 0,9 | |
| 0,85 | |
| 0,8 |
Регуляризация вариантов изменения параметров потоков отказов и восстановлений программного обеспечения и технических средств
Как было отмечено, при построении ВМЦ производится условная аппрСВГимация непостоянной функции λ(t) или μ(t) кусочно-непрерывной функцией. При этом после смены состояний системы происходит скачкообразное изменение величин λ или μ на определенные значения Δλ или Δμ. Следует отметить, что параметры Δλ и Δμ могут быть как постоянными величинами и приводить к линейному характеру изменения соответствующих интенсивностей, так и переменными. В последнем случае характер изменения интенсивностей проявления дефектов и восстановления будет носить нелинейный характер. Вид нелинейности можно определить после исследования характера и „веса” соответствующего дефекта. Само по себе такое определение представляет собой отдельную задачу.
Таким образом, для определения комбинаций вариантов изменения параметров потоков отказов и восстановлений необходимо перебрать случаи λ=const, λ=var, μ=const, μ=var, Δλ=0, Δλ=const, Δλ=var, Δμ=0, Δμ=const, Δμ=var. Результаты перебора сведены в таблицу 3.2.
Таблица 3.2 – Варианты изменения
параметров λ, μ, Δλ и Δμ
| № п/п | Λ | μ | Δλ | Δμ |
| Const | const | |||
| Var | const | const | ||
| Var | const | var | ||
| Const | var | const | ||
| Const | var | var | ||
| Var | var | const | const | |
| Var | var | const | var | |
| Var | var | var | const | |
| Var | var | var | var |
С помощью вариантов перебора, указанных в таблице 3.2, можно описать изменение параметров потоков отказов и восстановлений как АС, так и ПС. Однако условия решаемой задачи ограничивают область моделирования только множеством ДП ПС.
Возможные варианты изменения интенсивностей отказов и восстановлений ПС и величин их изменения удобно представить в виде дерева вариантов (рис. 3.1) и поставить ему в соответствие классификационную таблицу (таблица 3.3). Дерево составлено путем логических рассуждений и отражает полное множество вариантов, что подтверждается возможностью их перебора при принятых допущениях. Дерево вариантов отражает классификацию возможных вариантов изменения параметров и соответствующие им типы базовых макромоделей оценки надежности СВГ.
Рис. 3.1 – Комбинации вариантов изменения параметров λдп, μвп, Δλдп и Δμвп, определяющие вид БММ
В таблице 3.3 приведены классификационные признаки и поставленные им в соответствие числовые последовательности. Эти последовательности формализуют отображение множества вариантов рассматриваемых параметров во множество базовых макромоделей.
Таблица 3.3 – Классификационная таблица регуляризации вариантов изменения интенсивностей отказов,
восстановлений и величин их изменения
Дерево вариантов и классификационная таблица составлены в соответствии с четырьмя признаками. Первая цифра числовой последовательности определяет основные параметры λдп, μвп. Вторая – определяет номер варианта характера изменения параметров λдп и μвп. Третья – номер варианта изменения величин Δλдп и Δμвп. Четвертая – варианта изменения величин Δλдп и Δμвп. Полная числовая последовательность определяет основное содержание базовой макромодели. Таким образом, получены следующие варианты изменения параметров, определяющих надежностные характеристики ПС СВГ:
БММ №1 (1.2.1.1) – Δλдп – величина постоянная в каждом фрагменте, Δλдп i = const, i Î 1…N, где N – число фрагментов.
БММ №2 (1.2.1.2 и 1.2.2.1) – Δλдп – величина постоянная в зоне фрагментов, Δλдп i Î {Δλдп 0 ,…, Δλдп Nz}, где Nz – число зон фрагментов.
БММ №3 (1.2.2.2) – Δλдп – величина, изменяющаяся в каждом фрагменте, Δλдп Î {Δλдп i ,…, Δλдп N}, где N – число фрагментов.
БММ №4 (1.3.1.1) – Δμвп – величина постоянная в каждом фрагменте Δμвп i = const, i Î 1…N, где N – число фрагментов.
БММ №5 (1.3.1.2 и 1.3.2.1) Δμвп – величина постоянная в зоне фрагментов, Δμвп i Î {Δμвп 0 ,…, Δμвп Nz}, где Nz – число зон фрагментов.
БММ №6 (1.3.2.2) – Δμвп – величина, изменяющаяся в каждом фрагменте, Δμвп Î {Δμвп i,…,Δμвп N}, где N – число фрагментов.
БММ №7 (1.4.1.1) – в модели учитывается изменение величин λдп и μвп. Величины Δλдп и Δμвп постоянны в каждом фрагменете, где Δλдп i = const, Δμвп i = const, i Î 1…N, где N – число фрагментов
БММ №8 (1.4.2.1) – в модели учитывается изменение величин λдп и μвп. Величина Δλдп постоянна в каждом фрагменете, Δλдп i = const. Величина Δμвп постоянная в зоне фрагментов, Δμвп i Î {Δμвп 0 ,…, Δμвп Nz}, где Nz – число зон фрагментов.
БММ №9 (1.4.2.2) – в модели учитывается изменение величин λдп и μвп. Величина Δλдп постоянна в каждом фрагменете, Δλдп i = const. Величина Δμвп изменяется в каждом фрагменте, Δμвп Î {Δμвп i,…,Δμвп N}, где N – число фрагментов.
БММ №10 (1.4.3.1) – в модели учитывается изменение величин λдп и μвп. Величина Δμвп постоянна в каждом фрагменете, Δμвп i = const. Величина Δλдп постоянная в зоне фрагментов, Δλдп i Î {Δλдп 0,…,Δλдп Nz}, где Nz – число зон фрагментов.
БММ №11 (1.4.3.2) – в модели учитывается изменение величин λдп и μвп. Величина Δμвп постоянна в каждом фрагменете, Δμвп i = const. Величина Δλдп изменяется в каждом фрагменте, Δλдп Î {Δλдп i ,…, Δλдп N}, где N – число фрагментов.
БММ №12 (1.4.4.1) – в модели учитывается изменение величин λдп и μвп. Величины Δμвп и Δλдп изменяются в каждом фрагменте.
БММ №13 (1.4.4.2) – в модели учитывается изменение величин λдп и μвп. Величины Δμвп и Δλдп изменяются в зоне фрагментов.
Моделирование процесса функционирования вычислительной системы в рамках параметров БММ №1,2,4,5,7 достаточно легко реализуется при помощи математического аппарата марковских случайных процессов с непрерывным временем и дискретными состояниями. Вследствие учета изменения параметров lдп и mвп на величины Dlдп и Dmвп размерность задачи значительно возрастает, поэтому эффективность моделирования ВМЦ падает, что приводит к необходимости применения специальных методов, например имитационного моделирования.
Дата добавления: 2015-08-11; просмотров: 3111;
