ИСПОЛЬЗОВАНИЕ ФОРМАЛЬНО-ЛОГИЧЕСКИХ ЗАКОНОВ В ОБУЧЕНИИ

Формально-логические законы действуют во всяком мышле­нии, но в обучении особенно необходимо их сознательное исполь­зование, поскольку обучение направлено на формирование пра­вильного мышления у учащихся. При таком использовании зако­ны формальной логики выступают как нормативные правила мышления. Закон тождества как нормативное правило мышле­ния запрещает подменять в процессе рассуждения какое-либо понятие (или суждение) другим понятием (или суждением), запре­щает употреблять термины в различных смыслах, требует чет­кости, ясности и однозначности понятий. В работе преподавателя это проявляется в необходимости четкого определения вводимых понятий. В процессе обучения учащиеся встречаются с синонима­ми (око — глаз, болезнь — хворь) и омонимами (поле, класс, группа и др.). Употребление омонимов особенно опасно, если они имеют близкое значение. В преподавании отсутствие омони­мии — необходимое требование, ибо каждый термин или каж­дый знак (символ) должен определяться однозначно. В математи­ке ошибки иногда проистекают из того, что один и тот же термин употребляется в разных смыслах. Так, например, раньше запись [АВ] обозначала как отрезок с концами А и В, так и его длину; теперь этот отрезок обозначается через [АВ], а его длина — через \АВ\, при этом запись \АВ\ = 3см читается как «длина отрезка АВ равна 3 см». Слово «цифра» использовалось для обозначения соответствующего однозначного числа, что приводило к пута­нице при изложении материала.

Ясность и однозначность употребления понятий и символов в математике требуют особого математического языка, краткого | и точного, с правилами, которые в отличие от правил обычной грамматики не терпят никаких исключений. «С этой точки зрения, составление уравнений имеет сходство с переводом, перево­дом с обычного языка на язык математических символов» .

Анализируя новую задачу, учащиеся должны ввести подходя­щие обозначения. Д. Пойа считает, что хорошая система обозна­чений должна удовлетворять следующим требованиям: быть од­нозначной, содержательной, легко запоминающейся. Нельзя од­ним и тем же знаком обозначать разные объекты (в одной и той же задаче), но можно использовать различные символы для одного и того же объекта (например, конъюнкцию суждений можно обозначать как а&b, или а ^ b, или а • b). Учитель должен показать учащимся, что язык математических символов помога­ет ему в решении задач.

Закон тождества требует изложения материала, как устного, так и письменного, ясным и простым языком. Учебник должен помочь учащемуся выделить приниципиальное, отделить главное от второстепенного, не впадая в многословие, что сделать гораздо сложнее, чем на лекции или на уроке. Изложение в учебнике должно быть кратким, наглядным, логически четким, но не сухим.

Не менее важно использование закона тождества при изуче­нии родного или иностранного языка, литературы, истории и др. Закон тождества, как и в математике, требует однозначного употребления понятий, недопустимости логической ошибки «подмена понятия». К сожалению, люди путают некоторые поня­тия вследствие того, что не могут четко определить их содержа­ние (например, «приватизация», «индексация» и др.).

При изучении литературы учителя используют закон тождест­ва для обучения работе над сочинениями. Нарушение закона тождества проявляется в отступлении от обсуждаемой темы, в подмене одного предмета обсуждения другим. При написании сочинений требуется умение определять границы темы, отбирать соответствующий материал, развернуто и доказательно раскры­вать основную мысль сочинения. Недостатки в сочинениях про­являются в нарушении композиции (отсутствии вступления, вы­водов по теме, многословии, нарушении логики повествования). Законы логики (в том числе закон тождества) требуют ясности, сжатости изложения, умения полностью охватить тему сочине­ния, последовательности в изложении, правильного построения системы аргументации. Однако часть учащихся сужает тему, не умеет делать обобщений и выводов, находить подходящее слово из родного языка. Некоторые учащиеся отвечают на вопросы и передают содержание прочитанного «книжными» фразами, не могут кратко передать основную мысль «своими» словами (это относится и к переводу с иностранного языка на родной).

В ходе обучения в школе закон тождества используется и при проведении операции деления, а также для усвоения и построения различных классификаций, когда осуществляется требование постоянства признака, являющегося основанием деления или классификации. Нарушение этого требования приводит к логической ошибке, выражающейся в том, что члены деления не исключают друг друга.

На основании закона тождества осуществляется идентифика­ция, широко применяющаяся юристами-криминалистами, историками (в ходе изучения археологических раскопок), филологами, биологами, химиками, геологами, географами и т. д. При изуче­нии соответствующих наук преподаватели используют нужный материал, подтверждающий идентификацию (отождествление) различных объектов в ходе их изучения. Правильное отождествление дает нам знание об общих признаках предметов.

Закон тождества выражает отношение логической однозначно­сти, а закон непротиворечия — отношение логической несовмести­мости. Использование законов тождества и непротиворечия в школе тесно связано с операцией сравнения, в процессе которой устанавливаются сходства и различия рассматриваемых предметов. К. Д. Ушинский в своей педагогической деятельности отводил равнению одно из ведущих мест. При сравнении мы встречаемся двумя формами несовместимости: а и а (первая, более простая); а и b, где b распадается на не-а + с (вторая, более сложная). Закон непротиворечия охватывает обе эти формы несовместимости, форма а и 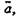примененная к суждениям, выражает отношения между суждениями А и О,Е и I(см. «логический квадрат»). Форма a и b выражает отношения между суждениями А и Е.

Закон непротиворечия используется в школе при осуществлении дихотомического деления понятий, когда мы понятие А делим на В и не-В (например, растения делятся на съедобные несъедобные). При этом В и не-В являются несовместимыми понятиями, находящимися в отношении противоречия (т. е. противоречащими понятиями). К несовместимым понятиям относятся и противоположные понятия (белая бумага — черная бумага; указание — награда, надежда — отчаяние). Закон непротиворечия, подобно закону тождества, распространяется не только на суждения, но и на понятия, а в логике классов — на классы, где он выражается формулой 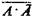[буквой А обозначается класс ( множество)]. Когда мы имеем дело с операцией дополнения классу А, обозначаемой 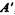, для которой действует закон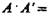 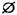(пересечение класса А с его дополнением пусто), то это лишь иная форма выражения закона непротиворечия применительно меннок понятиям, а не к суждениям.

Закон непротиворечия, примененный к понятиям, проявляется в использовании в письменной и устной речи слов-антонимов, отивоположных по своему основному значению и обозначающих противоположность тех или иных предметов, качеств, действий, состояний, явлений, желаний, результатов и т. д. (на­пример, великан — карлик, продление — сокращение, гармо­ния — дисгармония, симметрия — асимметрия, легкий труд — нелегкий труд и т. д.).

В зависимости от выражаемого типа противоположности антонимы делятся на следующие классы: 1. Антонимы, выража­ющие качественную противоположность. «Полную, истинную ан­тонимию выражают крайние симметричные члены такого проти­вопоставления, средние же указывают на возрастание (или убыва­ние) степени качества: легкий (простой, пустяковый), нетрудный, средней трудности, нелегкий, трудный (сложный)». 2. Антонимы, выражающие дополнительность. Это сравнительно небольшой класс антонимов, которые представляют собой два противополож­ных члена, дополняющих друг друга до выражения той или иной сущности, так что отрицание одного из них дает значение другого: не + холостой = женатый (слепой — зрячий, конечный — бесконеч­ный). 3. Антонимы, выражающие противоположную направлен­ность действий, признаков и свойств (разбирать — собирать, уве­личивать — уменьшать, зажигать — гасить, тушить и др.).

По способу образования слов антонимы можно подразделить с помощью дихотомического деления (т. е. на А и не-А) таким образом (рис. 41).

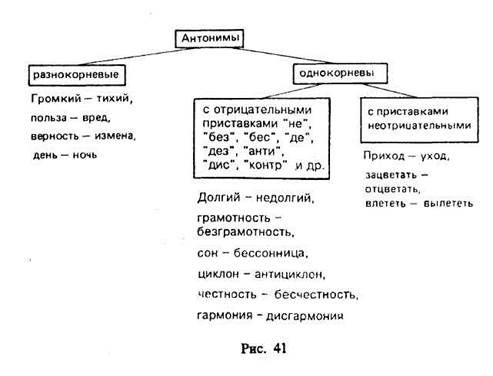
Антонимы могут выражаться с помощью формально различ­ных средств, поэтому одному слову может противопоставляться два или даже несколько слов. Например, в словаре М. Р. Львова имеются два антонима для слова «друг» — «враг», «недруг»; для слова «серьезный» антонимами являются слова «несерьезный», «легкомысленный»; для слова «благородный» — слова «низкий» (например, «благородный поступок» —- «низкий поступок»), «не­благородный» («благородный человек» — «неблагородный чело­век»), «низменный» («благородные побуждения» — «низменные побуждения»)¹⁴.

Из приведенных примеров видно, что несовместимые поня­тия, находящиеся в отношении противоречия или в отношении противоположности, могут выражаться словами-антонимами, имеющими разную структуру: 1) А—В (доброта — злоба; ге­рой — трус); 2) А — не-А (грамотность — неграмотность; вино­вность — невиновность).

Закон непротиворечия распространяется на понятия обоих видов и соответственно на антонимы указанных двух видов.

Задача учителя русского языка, литературы и других пред­метов состоит в том, чтобы во избежание нарушения закона непротиворечия тщательно следить за использованием антони­мов в письменной и устной речи. Следует отличать смысловые оттенки двух антонимов к одному и тому же слову (например, действие — бездействие, действие — противодействие; выгод­но — невыгодно, выгодно — убыточно).

На уроках литературы учащиеся знакомятся с отдельными проявлениями противоречивости в мышлении литературных ге­роев, учатся анализировать допущенные противоречия в своих сочинениях, в ответах своих одноклассников.

Если человек нечто утверждает, а затем то же самое отрицает, т. е. допускает противоречие, то он допускает ло­гическую ошибку.

В романе Тургенева «Рудин» есть такой диалог Рудина и Пигасова:

«— Прекрасно! — промолвил Рудин. — Стало быть, по-ва­шему, убеждений нет?

— Нет и не существует.

— Это ваше убеждение?

—Да.

— Как же вы говорите, что их нет? Вот вам уже одно, на первый случай.

Все в комнате улыбнулись и переглянулись».

В работе по развитию речи учителя используют различные методы, формы и средства обучения. В 5-м классе учащимся было дано задание подобрать дома открытку или репродукцию небольшого размера с изображением уголка природы, найти точные и яркие слова, словосочетания для описания этого предмета или явления. На уроке учащиеся смотрели через эпидиаскоп открытки и слушали описание того, что на них изображено. В одной из работ ученик написал: «Вся поляна наполнилась янтарным блеском. От берез и елей на землю падали унылые тени...» (на экране — соответствующее изображение открытки). Сразу поднимается множество рук, так как учащиеся замечают отсутствие яркого света на открытке. Оказалось, что ученик не знает значения слова «янтарный». Сообща находят синонимы: желтый, золотистый, золотисто-желтый. Смотрят на картину и видят, что такого освещения на ней нет. И уже сам ученик, автор сочинения, замечает, что «янтарный блеск» и «унылые тени» несовместимы.

В школьном преподавании отдельных предметов, и в первую очередь математики, часто используется метод «приведения к аб­сурду» (reductio ad absurdum). Применение этого метода в мате­матике основано на законе непротиворечия: если из допущения а вытекает противоречие, т. е. 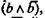то а должно быть отвергнуто, как ошибочное. Однако Д. Пойа приводит ряд аргументов, свидетельствующих о недостатках метода «приведения к абсур­ду» и метода косвенного доказательства, так как мы все время вынуждены концентрировать свое внимание не на истинной те­ореме, которую следует запомнить, а на ложном допущении, которое следует забыть. Словесная форма изложения, подчерки­вает Д. Пойа, может стать утомительной и даже невыносимой, так как неоднократно повторяются слова «гипотетически», «предположительно», «якобы»¹⁵ . Однако было бы неблагоразум­но совсем отказаться от «reductio ad absurdum» в математике, хотя лучше там, где возможно, заменить этот прием и метод косвенного доказательства прямым доказательством.

Закон непротиворечия используется в ходе проведения дис­путов в школе. Выдвинутое суждение одного учащегося и проти­воречащее ему суждение другого (например, Л и О) не могут быть одновременно и в одном и том же отношении истинными, одно из них обязательно ложно. В ходе дискуссии ложность одного суждения и должна быть доказана. Диспуты, в частности, применяются в процессе формирования читательских интересов школьников, наряду с обзорами новинок литературы, обсуждени­ями, конференциями и другими способами повышения уровня читательской культуры учащихся. Диспуты используются при обсуждении этических, эстетических и других проблем. Предме­том дискуссии становится вопрос, который в литературе и в жиз­ни разными людьми разрешается по-разному. Изучаемая пробле­ма допускает несколько толкований (например, нравственные проблемы), и в ходе дискуссии путем сравнения, анализа, обсуж­дения различных точек зрения учащиеся приходят к правильному выводу. Такие дискуссии можно проводить на уроках литерату­ры, истории. В ходе дискуссии учащиеся ставят остро волнующие их вопросы, приводят отрицательные факты и явления, заслужи­вающие общественного порицания (в частности, пьянство, воров­ство, взяточничество, вымогательство, должностные злоупотреб­ления и т. д.).

В процессе обучения используется и закон исключенного третьего, причем в многообразных ситуациях; мы же отметим лишь некоторые, наиболее важные. Закон исключенного третьего требует выбора одной из двух взаимоисключающих альтернатив.

Аналогично закону непротиворечия и закону тождества закон исключенного третьего применим не только к суждениям, но и к понятиям, а также к классам, выражающим объем понятия (формула 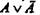для классов). В соответствии с этой формулой используется дихотомическое деление понятия на два взаимоиск­лючающих и взаимодополняющих (до универсума) класса. Дихо­томия используется во всех науках и соответственно в преподава­нии любой науки. Например, предложения бывают простыми или сложными (непростыми); внимание бывает произвольным или непроизвольным; числовой ряд конечным или бесконечным и т. д., и кроме этих А или не-А третьего не дано.

Дополнение к классу А, т. е. А', строится в соответствии с законом исключенного третьего и подчиняется формуле А+А'=1. На уроках математики эта формула и построение дополнения к классу А находит широкое применение.

На уроках по гуманитарным предметам учащиеся могут най­ти рассуждения литературных или исторических героев, постро­енные в соответствии с законом исключенного третьего. Вот пример: «Ломбард лихорадочно думал, выложить все начистоту или нет» (Агата Кристи).

В процессе обучения важную роль играет закон достаточного основания. Это выражается в требовании доказательности в изложе­нии учителя и в ответах учащихся, оптимального отбора информа­ции. В связи с тем, что в книге имеется отдельная глава «Логические основы аргументации», мы отсылаем читателя к ней (гл. VI).

Задачи к теме «Основные законы (принципы) правильного мышления»

I. Какие формально-логические законы распространяются на следующие пары суждений?

1. Все свидетели дают истинные показания.

Ни один свидетель не дает истинные показания.

2. «Статистика знает все» (И. Ильф, Е. Петров). Статистика знает не все.

3. Все кенгуру — сумчатые млекопитающие. Некоторые кен­гуру не являются сумчатыми млекопитающими.

4. Ни одна балалайка не является клавишным инструментом. Некоторые балалайки — клавишные инструменты.

5. «Арагонская хота» Глинки — увертюра-фантазия на ис­панские темы. «Арагонская хота» Глинки не является увертюрой-фантазией на испанские темы.

6. Нет человека, который не любил бы природу, не любо­вался бы на ясное, голубое небо. Некоторые люди не любят природу, не любуются на ясное, голубое небо.

II. Тождественны ли следующие понятия?

1. Гиппопотам. Носорог. Бегемот.

2. Крокодил. Аллигатор.

3. Композитор. Человек, сочинивший музыку.

4. Левитан. Художник, написавший картины «Март» и «Весна — большая вода». Художник, написавший картину «Грачи прилетели».

5. Упрямство. Порок слабого ума.

6. Французский физик Пьер Кюри (1859—1906). Ученый, сов­местно с женой М. Склодовской-Кюри открывший в 1898 г. полоний и радий. Лауреат Нобелевской премии (1903 г., совместно со Склодовской-Кюри).

III. Нарушен ли формально-логический закон в рекламе торгов­ца в следующей басне?

«Один торговец занимался продажей копий и щитов и, нахва­ливая свои щиты, кричал: «Вот самые крепкие щиты, ничто не сможет пробить их!» Тут же, расхваливая свои копья, он говорил: «Эти копья пробивают что угодно». Один из прохожих, услышав его слова, спросил: «А что будет, если попытаться проткнуть твой щит твоим же копьем?»¹⁶

IV. Какая логическая ошибка допущена в рассуждении Цандера? «С. П. Королев принес Цандеру путевку в санаторий в г. Кисловодск и предложил ему взять у врача разрешение на продление отпуска. Вечером С. П. Королев спросил у Цандера:

— Врач продлил вам отпуск?

— Да. Я говорю: «Продлите мне отпуск на неделю».

— А что такое? Зачем продлевать? — спрашивает врач.

— Устал.

— Что у вас за работа? На морозе или в горячем цеху? Что это вы так устали?

— Да нет, не на морозе. Я занимаюсь полетами на другие планеты.

— А-а, тогда понятно. Может, вам дать месяц? Соратники Цандера и Королев полегли со смеху. Только один человек не понимал, что здесь смешного, — это Цандер»¹⁷.

V. На действие каких формально-логических законов опирается Дж. X. Чейз в романе «Небезопасно быть свободным» в следу­ющих примерах?

1. «Тревожные мысли не оставляли ее, пока она одевалась, и, уходя из номера, она решила еще раз осмотреть его комнату в надежде обнаружить хоть что-нибудь, что либо успокоило бы ее, либо подтвердило подозрения».

2. «Если ты сообщишь отцу, то он, конечно, сразу же позво­нит в полицию. Если же ты ничего не скажешь, есть шанс, что никто никогда ни о чем не узнает. Поэтому я прошу тебя молчать».

3. «Флойд привык к ее постоянному вниманию. Его желания были и ее желаниями. Его потребности были ее потребностями. Но сегодня ночью он как будто для нее не существовал».

4. «— Она кого-нибудь спрашивала?

— Нет. Она прошла по холлу и поднялась по лестнице, как будто бы знала, куда ей нужно идти.

— Она не ехала на лифте?

— Нет.

— Тогда, скорее всего, номер, куда она направлялась, нахо­дится на первом или на втором этаже. Ведь, чтобы подняться на третий этаж, ей пришлось бы воспользоваться лифтом».

5. «Надо снять отпечатки пальцев и проверить, совпадают ли они с отпечатками, которые мы нашли на другой бусине».

6. «— Тот отпечаток, который мы нашли на бусине в гости­нице «Плаза», не соответствует отпечаткам пальцев Керра».

7. «— Очень интересно, комиссар. Мне удалось найти от­печаток на лампе, совпадающий с тем, который оставлен на бусине. Это вне сомнения».

VI. Льюис Кэрролл в своих сказках об Алисе неоднократно показывал действие законов формальной логики. Какие законы нашли отражение в приведенных ниже отрывках?

1. «— Если бы кое-кто не совался в чужие дела, — хрипло проворчала Герцогиня, — земля бы вертелась быстрее!

— Ничего хорошего из этого бы не вышло, — сказала Алиса, радуясь случаю показать свои знания. — Только представьте себе, что бы сталось с днем и ночью. Ведь земля совершает оборот за двадцать четыре часа...

— Оборот? — повторила Герцогиня задумчиво. И, повернув­шись к кухарке, прибавила:

— Возьми-ка ее в оборот! Для начала оттяпай ей голову!»

2. «— Заговорить с ней или нет? — подумала Алиса».

3. «Алиса постаралась представить себе, как выглядит пламя свечи после того, как свеча потухнет. Насколько ей помнилось, такого она никогда не видела».

4. Алиса сказала: «Какой сегодня день странный! А вчера все шло как обычно! Может, это я изменилась за ночь? Дайте-ка вспомнить: сегодня утром, когда я встала, я это была или не л? Кажется, уже не совсем я! Но если это так, то кто же я в таком случае? Это так сложно...»i

VII. Всему миру известен город Габрово в Болгарии, жители которого щедро одарены чувством юмора. Нарушение каких законов отражено в следующих габровских анекдотах?

1. «Какая температура в комнате? — спросил муж у жены. «Пятнадцать градусов», — ответила его жена. «А на улице?» —«Двадцать». — «Тогда открой окно, — распорядился муж, — пусть войдут еще пять градусов».

2. Габровский анекдот под названием «Реклама»: «— Значит, это самая новая ткань?

— Только вчера получил, прямо с фабрики!

— А она не линючая?

— Да что вы! Больше месяца висела на витрине, и ничего ей не сделалось!»

VIII. Какие законы формальной логики отражены в этом от­рывке?

«Чертог вдовы Грицацуевой сиял. Во главе свадебного стола сидел марьяжный король — сын турецко-подданного. Он был элегантен и пьян. Гости шумели. Молодая была уже не молода. Ей было не меньше тридцати пяти лет» (И. Ильф, Е. Петров).