Пересечение («умножение») классов
Общей частью, или пересечением, двух классов называется класс тех элементов, которые содержатся в обоих данных множествах, т. е. это множество (класс) элементов, общих обоим множествам18. Пересечение обозначается 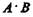 или
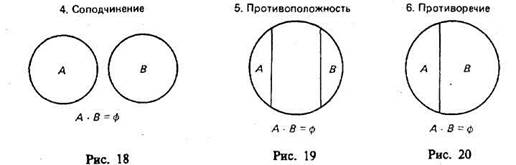
или 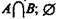 — пустое множество. При пересечении могут встретиться следующие 6 случаев (рис. 15—20, где результат пересечения заштрихован).
— пустое множество. При пересечении могут встретиться следующие 6 случаев (рис. 15—20, где результат пересечения заштрихован).
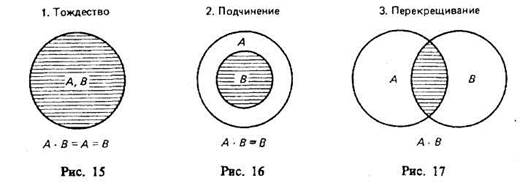
Например, операция пересечения классов «школьник» (А) и «футболист» (В) заключается в нахождении таких людей, которые одновременно являются и школьниками, и футболистами. Это изображено на рис. 17, где общая часть классов А и В заштрихована.
Основные законы логики классов. Законы операций объединения и пересечения
1. Законы идемпотентности.
А + А = А. А х А = А.
В школьном курсе алгебры таких законов нет. В логике первый из этих законов означает следующее. Если мы к классу «дом» прибавим класс «дом», то получим класс «дом», т. е. домов не станет в два раза больше и объем понятия «дом» останется прежним.
2. Законы коммутативности. Эти законы существуют в алгебре, в арифметике, в теории множеств и в логике классов.
А + В = В+А. А В=В А.
Если мы к классу «растение» прибавим класс «животное», то получим класс «организм»; тот же самый класс получим, если мы к классу «животное» прибавим класс «растение».
3. Законы ассоциативности. Они существуют в арифметике, алгебре, теории множеств и в логике классов.
(А+В) + С = А + (В+С). (A х B) х C=A х (B х С).
4. Законы дистрибутивности.
(A+B)C=(A х С)+(B х С). (A х B) + C=(A + С) х (B+С).
5. Законы поглощения. Этих законов нет в арифметике и в школьном курсе алгебры.
А + (А х В)=А. А х (А+В)=А.
Доказательство этих законов осуществляется графическим методом. Два закона поглощения для «сложения» и «умножения» классов иллюстрируются графически на рис. 21 и 22.
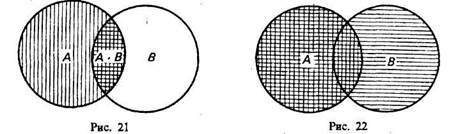
Промежуточный результат изображен горизонтальной штриховкой. В первом законе поглощения он равен А В, а во втором — равен А + В. Конечный результат изображен вертикальной штриховкой; он равен классу А.
Дата добавления: 2015-08-11; просмотров: 878;
