Вычитание классов
Рассмотрим два множества (класса) А и В, из которых В может и не быть частью А. Разностью множеств (классов) А и В называется множество тех элементов класса А, которые не являются элементами класса В. Разность обозначается А —В.
Могут встретиться следующие пять случаев (если классы А и В не пусты и не универсальны).
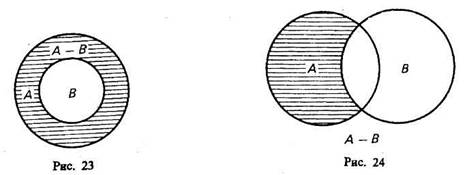
1-й случай (рис. 23). Класс А включает в себя класс В. Тогда разностью А — В будет заштрихованная часть А, т. е. множество тех элементов, которые не суть В. Например, если мы из множества звуков русского языка (А) вычтем множество гласных звуков (В), то получим множество согласных звуков, изображенное на чертеже в виде заштрихованного кольца.
2-й случай (рис. 24). Разностью двух перекрещивающихся классов будет заштрихованная часть А. Например, разность множеств «рабочий» (А) и «рационализатор» (В) даст множество рабочих, которые не являются рационализаторами.
3-й случай (рис. 25). Если класс А полностью включен в класс В и класс В полностью включен в класс А, то эти классы (множества) равны (тождественны). Тогда разность А -В даст пустой, или нулевой, класс, т. е. класс, в котором нет ни одного элемента. Например, если мы из класса «сосна» вычтем класс «сосна», то разность А—В будет равна пустому классу.
4-й случай (рис. 26). Класс А и класс В не имеют общих элементов.
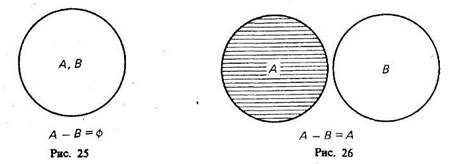
Тогда разность А—В=А, так как всякий элемент класса А не является элементом класса В. Например, разность класса «стол» (А) и класса «стул» (В) равна классу «стол» (А).
В результате «вычитания» классов, соответствующих понятиям, находящимся в отношении противоположности [«низкий дом» (А), «высокий дом» (В)] или противоречия [«одушевленный предмет» (А), «неодушевленный предмет» (В)], разность А— В также равна А (рис. 27, 28).
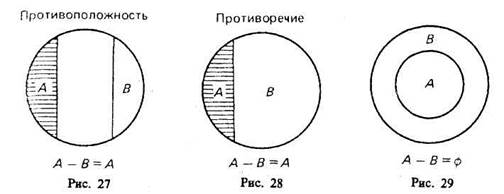
5-й случай (рис. 29). Если объем класса А меньше объема класса В, то в результате вычитания получим пустой класс, так как нет элементов класса А, которые не являлись бы элементами класса В. Например, разность класса «личное местоимение» (А) и «местоимение» (В) дает пустой класс.
Для операции вычитания классов справедливы следующие законы:
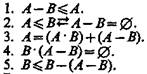
В интерпретации логических алгебр посредством классов запись 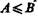 обозначает включение класса А в класс В;
обозначает включение класса А в класс В; 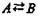 обозначает эквивалентность классов (А тогда и только тогда, когда В ).
обозначает эквивалентность классов (А тогда и только тогда, когда В ).
Дата добавления: 2015-08-11; просмотров: 784;
