Способ прямоугольных координат

Порядок разбивки данным способом следующий.

1. Задавшись длиной дуги S (расстояние между соседними точками разбивки), приняв нк или кк за начало координат, направление тангенсов на вершину угла за направление оси Х, вычисляют координаты точек кривой по формулам, очевидным из рис. 94.

2. По φ и R определяют главные элементы кривой – Т (тангенс, касательная к кривой), Б (биссектриса), К (длина кривой), Д (домер).

3. Закрепляют главные точки кривой – нк, ск, кк.

Для этого от вершины угла при помощи рулетки по направлению к началу трассы откладывают Т. Полученная точка является нк и закрепляется деревянным колышком. Затем откладывают Т от ВУ по направлению на последующее направление трассы, получают таким образом кк, которую тоже закрепляют колышком. Внутренний угол при помощи теодолита делят пополам и на полученном направлении откладывают Б, получают ск.

φ – угол поворота трассы (в данном случае вправо); ВУ – вершина угла; нк – начало кривой; кк – конец кривой; ск – середина кривой. Эти точки называют главными точками кривой. R – радиус кривой.

Х Х

φ

ВУ

ск

S S

нк S

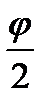S кк

R

φ

У У

О

Рис. 94. Главные точки горизонтальной круговой кривой

у₁=R-R·cosβ=R·(1-cosβ)=2R·sin² 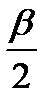; х₁=R·sinβ; у₂=2R·sin²β; х₂=R·sin2β; х_n=R·sinβ

у_n=2R·sin^{2 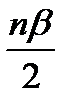;} β= 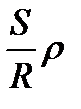, ρ – радиан, единица плоского угла =206265″.

Значения х_n, у_n можно выбирать из таблиц для разбивки круговых кривых.

4. Вдоль тангенсов от нк и кк откладывают при помощи рулетки значения х_n по перпендикуляру у_n и закрепляют полученные точки колышками.

Х

на ВУ

х₂ х₃ 2

х₁ 1

нк S

у₁ S S

у₂

у₃ β β

R β

У О

Рис. 95. Разбивка способом прямоугольных координат