Параллельный колебательный контур. Резонанс токов.
Рассмотрим цепь, состоящую из параллельно включенных активного, индуктивного и емкостного сопротивлений.
Из этого выражения видно, что взаимная компенсация реактивных проводимостей (угол 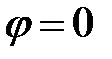 ) достигается при условии когда:
) достигается при условии когда:  , притом, что
, притом, что  .
.
При резонансе реактивная проводимость цепи b = 0. Поэтому полная проводимость y достигает минимального значения. Поэтому ток в общей ветви при неизменном напряжении так же минимален.
Векторная диаграмма при резонансе имеет вид:
IL= 
|
| Общий вектор тока является геометрической суммой векторов трех токов, два из которых IL и IC находятся в противофазе. Следовательно, возможны случаи, когда токи в индуктивной катушке и конденсаторе могут значительно превосходить суммарный ток в цепи. Поэтому резонанс при параллельном соединении называют резонансом токов.
|
Энергетические процессы в параллельной цепи аналогичны соответствующим процессам в последовательной цепи, т.е. и в этом случае происходят колебания энергии в цепи. Энергия полей переходит из конденсатора в катушку и обратно. Источник энергии покрывает потери энергии в ветви с активной проводимостью.
Дата добавления: 2015-08-11; просмотров: 868;
 ,
, 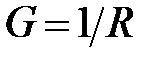 .
Угол сдвига фаз:
.
Угол сдвига фаз:
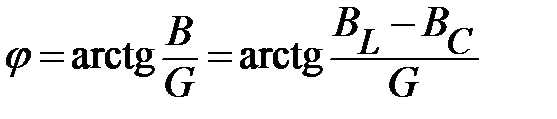 .
Модуль проводимости:
.
Модуль проводимости:  .
.
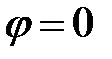 ) достигается при условии когда:
) достигается при условии когда:  , притом, что
, притом, что  .
.
