Комплексный метод расчета электрических цепей
Существенное упрощение достигается изображением синусоидальных функций времени комплексными числами.
Существует несколько форм представления комплексного числа:
- алгебраическая форма: 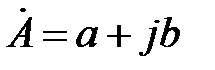 ;
;
- показательная (или экспоненциальная) форма: 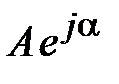 ;
;
- тригонометрическая форма: 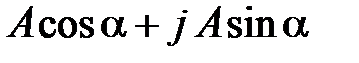 .
.
Все эти формы связаны между собой, в частности, модуль числа 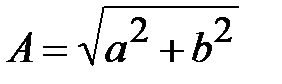 , аргумент
, аргумент 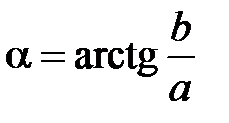 .
.
| Для геометрического изображения используют прямоугольную систему координат, в которой по горизонтальной оси откладываются вещественные числа, а по вертикальной – мнимые:
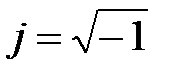 ; ; 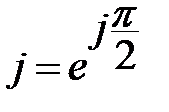 ; ; 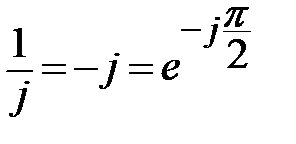 . .
|
Для вещественной и мнимой частей комплексного числа употребляют также обозначения: 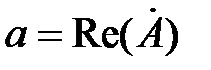 ,
, 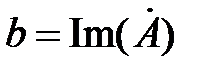 .
.
Две комплексные величины, имеющие равные модули и равные, но противоположные по знаку аргументы, называют сопряженными.
Если 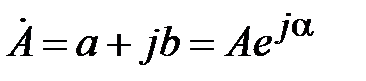 , то сопряженное ему комплексное число запишется в форме
, то сопряженное ему комплексное число запишется в форме 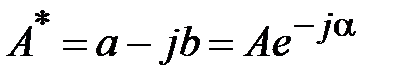 . При этом соблюдается равенство:
. При этом соблюдается равенство: 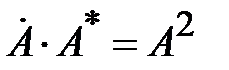 .
.
Полезно помнить, что 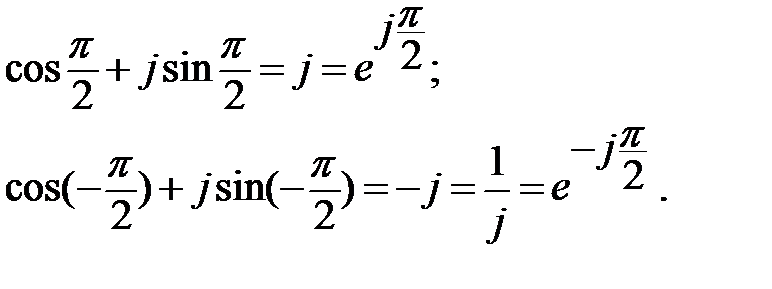
Пусть имеем синусоидально изменяющийся ток с начальной фазой φi 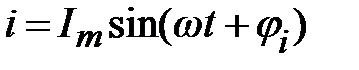 .
.
Его можно представить в форме 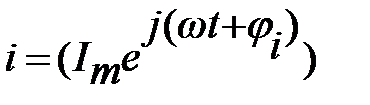 .
.
Таким образом, синусоидальный ток рассматривают как комплексное изображение синусоидального тока, которое при заданной частоте ω определяется двумявеличинами – амплитудой и начальной фазой:
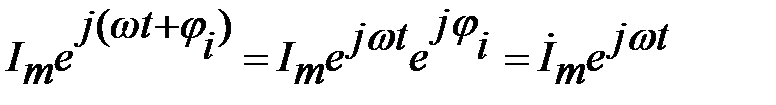 .
.
Здесь комплексное число 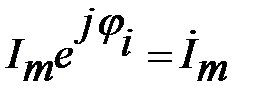 называют комплексной амплитудой тока.
называют комплексной амплитудой тока.
Рассмотрим теперь выражение для производной по времени от синусоидального тока:
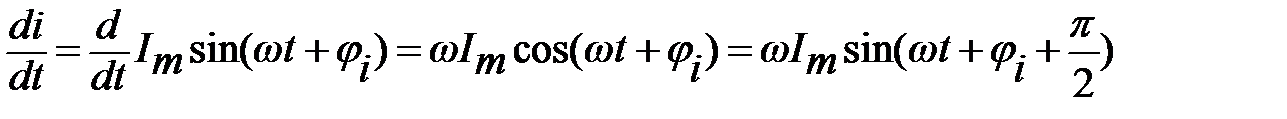 .
.
Изображение производной будет иметь вид:
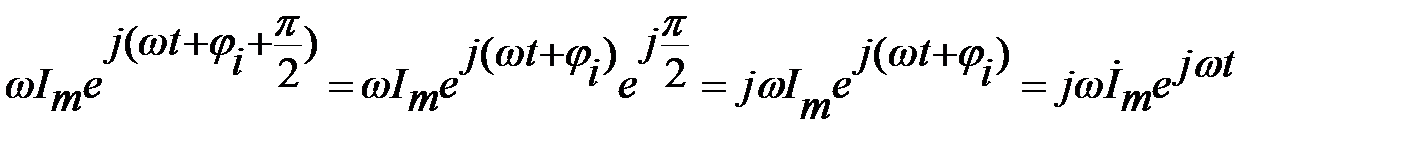 .
.
Таким образом, операция дифференцирования действительной функции заменяется умножением ее комплексного изображения на 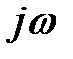 .
.
Рассмотрим изображение интеграла от синусоидальной функции
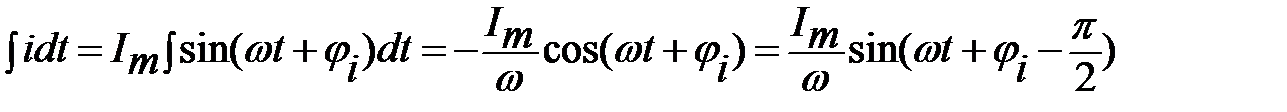 .
.
Искомое изображение интеграла будет иметь вид:
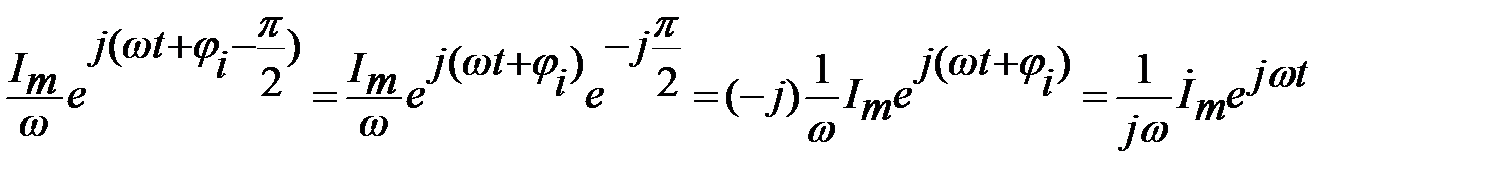 .
.
Следовательно, операция интегрирования действительной функции заменяется делением ее комплексного изображения на 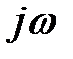 .
.
Таким образом, комплексный метод позволяет заменить интегро-дифференциальное уравнение, содержащее функции времени, алгебраическим уравнением с их комплексными изображениями.
Алгоритм метода:
1. Замена заданных функций времени их комплексными изображениями.
2. Замена всех уравнений, составленных по закону Кирхгофа, алгебраическими уравнениями для комплексных изображений.
3. Нахождение комплексных изображений искомых функций.
4. Переход к оригиналам этих функций.
В качестве примера рассмотрим цепь с последовательно соединенными элементами R,L и C,к зажимам которой приложено напряжение, изменяющееся по синусоидальному закону 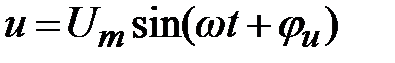 . Требуется найти ток в цепи:
. Требуется найти ток в цепи: 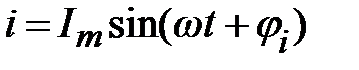 .
.
| |
1) Заменяем функции времени их изображениями: 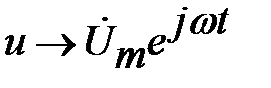 ,
, 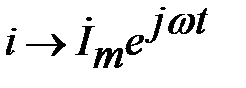 .
.
2) Составляем уравнение по второму закону Кирхгофа:
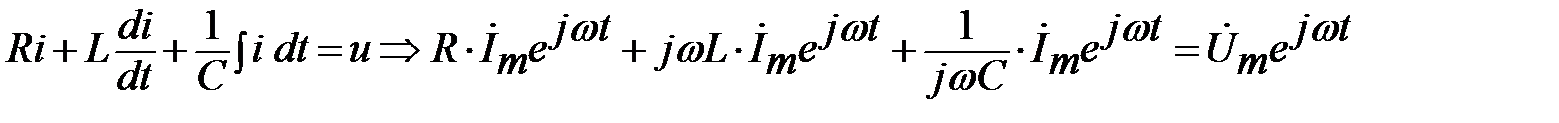 .
.
Полученное уравнение является алгебраическим. Все слагаемые имеют общий множитель 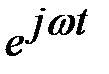 . Окончательно получаем уравнение в комплексных амплитудах:
. Окончательно получаем уравнение в комплексных амплитудах:
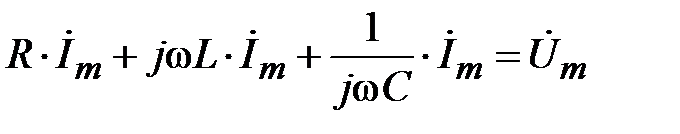 .
.
3) Из последнего уравнения легко определяется комплексная амплитуда тока:
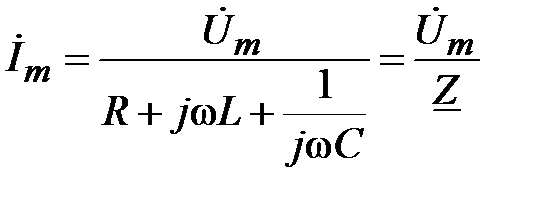 ,
,
где 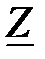 – комплексное сопротивление цепи.
– комплексное сопротивление цепи.
4) Зная выражение для комплексной амплитуды тока в виде 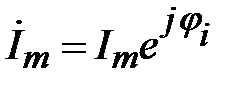 , можем, используя обратный переход, записать выражение для мгновенного тока:
, можем, используя обратный переход, записать выражение для мгновенного тока: 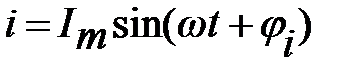 .
.
Обычно рассматривают действующие значения токов и напряжений. Так как действующие синусоидальные токи и напряжения меньше их амплитуд в 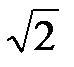 раз, то обычно вместо комплексных амплитуд рассматривают комплексные действующие величины:
раз, то обычно вместо комплексных амплитуд рассматривают комплексные действующие величины: 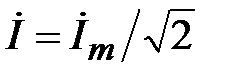 ,
, 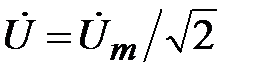 .
.
Дата добавления: 2015-08-11; просмотров: 905;