Пример. Динамика производства стиральных машин Месяц Стиральные машины Трехчленные скользящие суммы Трехчленные скользящие средние
Динамика производства стиральных машин
| Месяц | Стиральные машины | Трехчленные скользящие суммы | Трехчленные скользящие средние | Четырех членные суммы | Четырех членные скользящие | Четырехчленные Скользящие (центрированные) |
| - | - | - | - | - | ||
| 161,67 | - | 154,00 | - | |||
| 153,67 | - | 154,75 | 154,4 | |||
| 152,00 | 150,75 | 152,8 | ||||
| 145,33 | 141,50 | 146,1 | ||||
| 145,00 | 145,00 | 143,3 | ||||
| 140,67 | 137,50 | 141,3 | ||||
| 134,33 | 135,75 | 136,6 | ||||
| 137,67 | 143,00 | 139,4 | ||||
| 142,33 | 146,75 | 144,9 | ||||
| 153,00 | 151,50 | 149,1 | ||||
| 155,33 | 154,00 | 152,8 | ||||
| 152,33 | 155,50 | 154,8 | ||||
| 154,00 | - | - | ||||
| - | - | - |
3. Аналитическое выравнивание. Под этим понимают определение основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает перед исследователем как бы в зависимости только от течения времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически. В результате приходят к трендовой модели
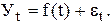
где f(t)- уровень, определяемый тенденцией развития;
et - случайное и циклическое отклонение от тенденции.
Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t). На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.
Чаще всего при выравнивании используются следующие зависимости:
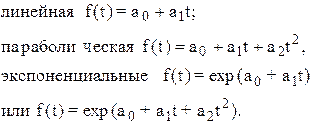
Линейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.
Параболическая зависимость используется, если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.
Экспоненциальные зависимости применяются, если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, - устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста, цепных коэффициентов роста цепных же коэффициентов или темпов роста и т. п.).
Оценка параметров (a0, a1, a2,...) осуществляется следующими методами:
1) методом избранных точек,
2) методом наименьших расстояний,
3) методом наименьших квадратов (МНК).
В большинстве расчетов используют метод наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выравненных:
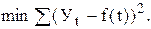
Для линейной зависимости (f(t)=a0+a1t) параметр а0 обычно интерпретации не имеет, но иногда его рассматривают как обобщенный начальный уровень ряда; а1 - сила связи, т.е. параметр, показывающий, насколько изменится результат при изменении времени на единицу. Таким образом, а можно представить как постоянный теоретический абсолютный прирост. Построив уравнение регрессии, проводят оценку его надежности. Это делается посредством критерия Фишера (F). Фактический уровень (Fфакт) сравнивается с теоретическим (табличным) значением:

где k - число параметров функции, описывающей тенденцию;
n - число уровней ряда;
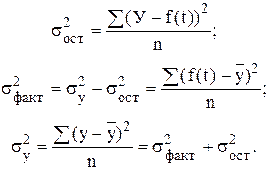
Fфакт сравнивается с Fтеор при v1 = (k - 1), v2 = (n - k) степенях свободы и уровне значимости a (обычно a = 0,05). Если Fфакт > Fтеор, уравнение регрессии значимо, т.е. построенная модель адекватна фактической временной тенденции.
Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров уравнения.
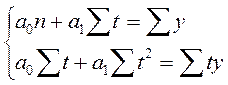

где y – исходный уровень ряда динамики,
n – число членов ряда,
t –показатель времени, который обозначается порядковыми номерами, начиная от низшего.
Решение системы уравнений позволяет получить выражения для параметров уравнения.
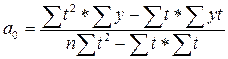
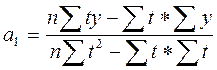
С целью упрощения расчетов показателям времени t придают такие значения, чтобы их сумма была равна 0. Тогда уравнения параметров примут следующий вид:
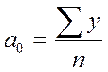 ,
, 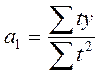 .
.
| Год | Производство молока в регионе, млн. т. | Условные годы, t | Расчет параметров уравнения | Оценка модели | |||
| t | t2 | Y·t | Yt | Y - Yt | (Y-Yt)2 | ||
| 13,3 | -2 | -26,6 | 13,02 | 0,28 | 0,08 | ||
| 13,5 | -1 | -13,5 | 13,94 | -0,44 | 0,19 | ||
| 14,8 | 14,86 | -0,06 | 0,00 | ||||
| 16,1 | 16,1 | 15,78 | 0,32 | 0,10 | |||
| 16,6 | 33,2 | 16,7 | -0,1 | 0,01 | |||
| 74,3 | 9,2 | 74,3 | - | 0,39 |
| Год | Производство молока в регионе, млн. т. | Условные годы, t | Расчет параметров уравнения | Оценка модели | |||
| t | t2 | Y·t | Yt | Y - Yt | (Y-Yt)2 | ||
| 13,3 | 13,3 | 13,02 | 0,28 | 0,08 | |||
| 13,5 | 13,94 | -0,44 | 0,19 | ||||
| 14,8 | 44,4 | 14,86 | -0,06 | 0,00 | |||
| 16,1 | 64,4 | 15,78 | 0,32 | 0,10 | |||
| 16,6 | 16,7 | -0,1 | 0,01 | ||||
| 74,3 | 232,1 | 74,3 | - | 0,39 |
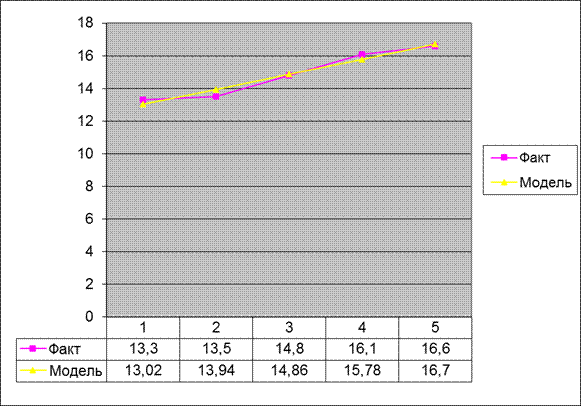

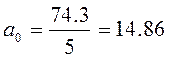

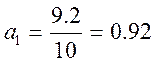

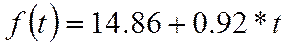
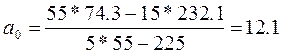
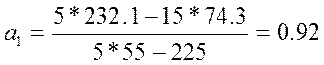
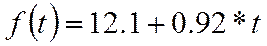
 Для определения колеблемости рассчитывается показатель среднего квадратического отклонения:
Для определения колеблемости рассчитывается показатель среднего квадратического отклонения:
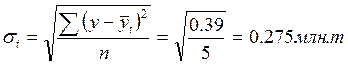
Относительной мерой колеблемости является коэффициент вариации:
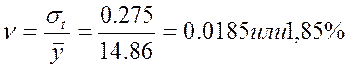
Если число уровней ряда четное, то условное обозначение показателя времени приме следующий вид:
| Год | ||||||
| t | - 5 | - 3 | - 1 |
( счет времени ведется полугодиями)
При аналитическом выравнивании по параболе система уравнений для определения ее параметров примет следующий вид:
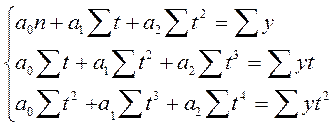
При  система примет вид:
система примет вид:

Дата добавления: 2015-08-11; просмотров: 1015;
