Показатели анализа рядов динамики
При изучении явления во времени перед исследователем встает проблема описания интенсивности изменения и расчета средних показателей динамики. Решается она путем построения соответствующих показателей. Для характеристики интенсивности изменения во времени такими показателями будут:
1) абсолютный прирост,
2) темпы роста,
3) темпы прироста,
4) абсолютное значение одного процента прироста.
Расчет показателей динамики представлен в следующей таблице.
| Показатель | Базисный | Цепной |
Абсолютный прирост  *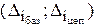
| Yi-Y0 | Yi-Yi-1 |
| Коэффициент роста (Кр) | Yi : Y0 | Yi : Yi-1 |
| Темп роста (Тр) | (Yi : Y0)×100 | (Yi : Yi-1)×100 |
| Коэффициент прироста (Кпр )** |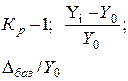 
| 
|
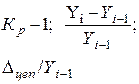
| Темп прироста (Тпр) |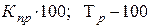 
|
|
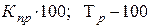
| Абсолютное значение одного процента прироста (А) |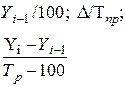 
|
* 
** 
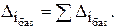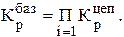
В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях.
Рассмотрим пример. Имеются данные об объемах и динамике продаж мясных консервов в регионе за ряд лет:
| Годы | Консервы мясные, млн. усл. банок | Абсолютные приросты, млн. усл. банок | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста, млн. усл. банок | |||
| цепные | базисные | цепные | базисные | цепные | базисные | |||
| 891,00 | - | - | - | - | - | - | - | |
| 806,00 | -85,00 | -85,00 | 90,5% | 90,5% | -9,5% | -9,5% | 8,91 | |
| 1595,00 | 789,00 | 704,00 | 197,9% | 179,0% | 97,9% | 79,0% | 8,06 | |
| 1637,00 | 42,00 | 746,00 | 102,6% | 183,7% | 2,6% | 83,7% | 15,95 | |
| 1651,00 | 14,00 | 760,00 | 100,9% | 185,3% | 0,9% | 85,3% | 16,37 | |
| 6580,00 | 760,00 | 185,3% |
Система средних показателей динамики включает:
средний уровень ряда,
средний абсолютный прирост,
средний темп роста,
средний темп прироста.
Средний уровень ряда - это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности. Расчет среднего уровня ряда динамики определяется видом этого ряда и величиной интервала, соответствующего каждому уровню.
Для интервальных рядов с равными периодами времени средний уровень Y рассчитывается следующим образом:
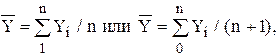
где n или (n +1) - общая длина временного ряда или общее число равных временных отрезков, каждому из которых соответствует свой уровень Yi (1 = 1, 2,...,n или 1 = 0, 1, 2,..., n).
В нашем примере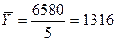 
млн.усл.банок.
Для интервального ряда с неравноотстоящими уровнями
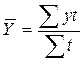, где t – число периодов времени, в течение которых уровень не изменялся.
Для моментного ряда с равноотстоящими уровнями средняя хронологическая определяется по формуле:
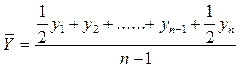, где n – число уровней ряда.
Для моментного ряда с неравноотстоящими уровнями средняя хронологическая рассчитывается:
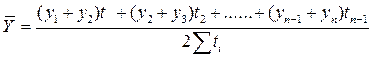
Средний абсолютный прирост рассчитывается по цепным абсолютным приростам по формуле:
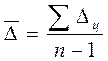или
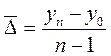
Для нашего примера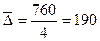 
млн.усл.банок.
Средний темп роста:
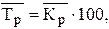
где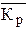 
- средний коэффициент роста, рассчитанный как
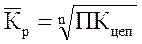или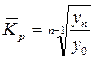 
Здесь Кцеп - цепные коэффициенты роста.
Для нашего примера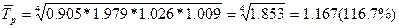 
Средний темп прироста (%) определяется по единственной методологии:
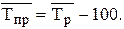
Дата добавления: 2015-08-11; просмотров: 846;