Схема раздельного резервирования
1.19 Расчёт надёжности системы с постоянным резервированием
При постоянном резервировании резервные элементы 1,2,.....,m соединены параллельно с основным (рабочим) элементом в течении всего периода работы системы. Все элементы соединены постоянно, перестройка схемы при отказах не происходит, отказавший элемент не отключается.
Определим вероятность отказа системы.
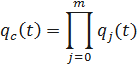
Вероятность безотказной работы системы.

Будем называть элементы системы равнонадёжными, если
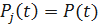 ;
; 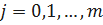
Для равнонадёжных элементов имеем
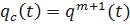
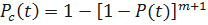 .
.
При экспоненциальном законе надёжности отдельных элементов имеем
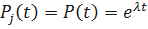 .
.
Тогда
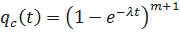 ;
; 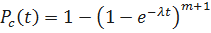 .
.
Определим среднее время безотказной работы резервированной системы
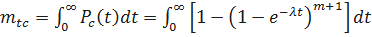 .
.
Введём новую переменную x вида 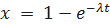 ;
;
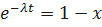 ;
; 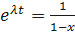 ;
; 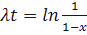 ;
;
Если 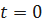 , то
, то  ;
;
Если 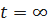 , то
, то 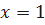 ;
;
В результате получим
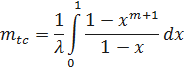
Запишем формула для определения суммы n членов геометрической прогрессии
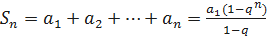 ;
;
где 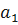 – первый член суммы;
– первый член суммы; 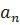 - n-ый член суммы; q – знаменатель прогрессии;
- n-ый член суммы; q – знаменатель прогрессии;
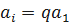 ,
, 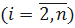 ;
; 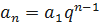 .
.
Выражение
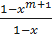 ;
;
Есть сумма n членов геометрической прогрессии, где 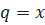 ;
; 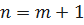 ;
; 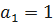 ;
; 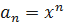 .
.
Следовательно
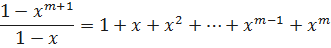
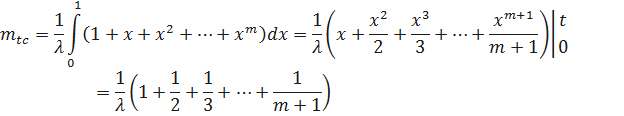
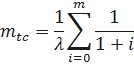
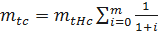 ,
, 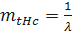
где 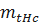 - среднее время безотказной работы нерезервированной системы.
- среднее время безотказной работы нерезервированной системы.
Введём обозначение
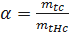 ;
;
Для разных значений m имеем
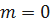 ;
; 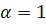
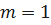 ;
; 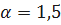
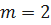 ;
; 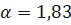 .
.
Результаты сведём в таблицу
По данным таблицы строим график зависимости 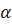 , от
, от 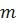 .
.
1.20 Расчёт надёжности системы с постоянным общим резервированием
Резервирование называется общим, если резервируется вся система, состоящая из последовательного соединения nэлементов.
Основная цель содержит nэлементов.
Число резервных цепей равно m, кратность резервирования равна m. Общее число резервных элементов равно mn.
Определим количественные характеристики надёжности в случае постоянного включения резервных цепей.
Введём обозначения
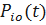 ,
, 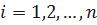 – вероятность безотказной работы элемента io;
– вероятность безотказной работы элемента io;
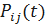 ,
, 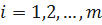 ;
; 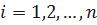 – вероятность безотказной работы элемента ij;
– вероятность безотказной работы элемента ij;
Запишем вероятность безотказной работы j-ой цепи
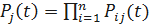 ;
; 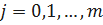 ;
;
Вероятность отказа j-ой цепи
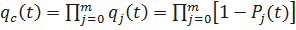 .
.
Подставим (1.7) в (1.9). Получим
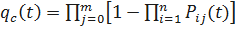 .
.
Определим вероятность безотказной работы системы
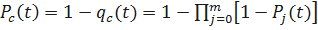 .
.
Частный случай: основная и резервные цели имеют одинаковую надёжность, т.е.
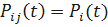 .
.
Тогда
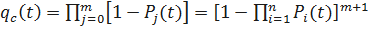 ;
;
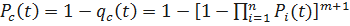 ;
;
Рассмотрим экспоненциальный закон надёжности, т.е.
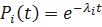 ;
;
Тогда 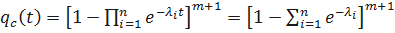 ;
;
или 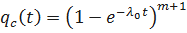
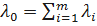 – интенсивность отказов цепи, состоящей из nэлементов.
– интенсивность отказов цепи, состоящей из nэлементов.
Вероятность безотказной работы системы.
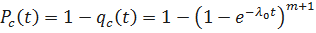 ;
;
Определим интенсивность отказов системы
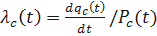 ;
;
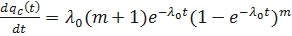 ;
;
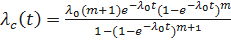 ;
;
Определим среднее время безотказной работы резервированной системы
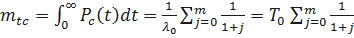 ;
;
где 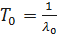 – среднее время безотказной работы нерезервированной системы.
– среднее время безотказной работы нерезервированной системы.
Т.о. с увеличением кратности резервирования mсреднее время безотказной работы растёт, но очень медленно. Наибольший прирост наблюдается при переходе от нервированной системы к резервированной с кратностью 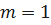 .
.
1.21 Расчёт надёжности системы с постоянным поэлементным резервированием
При поэлементном резервировании резервируются отдельные элементы системы.
Определим количественные характеристики надёжности системы.
Введём обозначения:
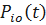 ,
, 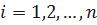 – вероятность безотказной работы элемента ij на интервале времени (0, t).
– вероятность безотказной работы элемента ij на интервале времени (0, t).
Запишем вероятность отказа i-ой группы.
Имеем 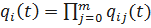 ,
, 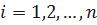 .
.
Запишем вероятность безотказной работы i-й группы. Имеем
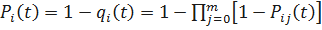 .
.
Запишем вероятность безотказной работы системы с поэлементным резервированием
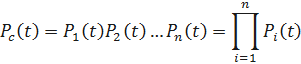
или
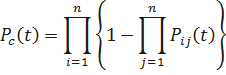
Для равнонадёжных элементов системы имеем: 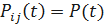
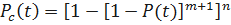 ;
;
1.20 Режим облегченного (тёплого) резерва
Рассмотрим случай, когда время безотказной работы всех элементов изделия подчиняется экспоненциальному закону распределения. В этом случае процессы, характеризующие работу изделия являютсямарковскими. Для определения характеристик надёжности можно использовать математический аппарат теории марковских случайных процессов.
В режиме облегченного резерва резервные элементы находятся в режиме недогрузки до момента их включения в работу. Пусть 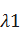 - интенсивность отказа резервного элемента в режиме недогрузки до момента их включения в работу.
- интенсивность отказа резервного элемента в режиме недогрузки до момента их включения в работу. 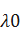 - интенсивность отказа резервного элемента в состоянии работы.
- интенсивность отказа резервного элемента в состоянии работы.
Введём в рассмотрение состояния 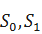 ,
, 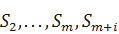 .
.
S0 - основной элемент исправен и работает, ш резервных элементов исправны и находятся в режиме недогрузки.
S1 - основной элемент отказал, работает 1 - ый резервный элемент, (m – 1) резервные элементы исправны и находятся в режиме недогрузки.
S2 - отказал 1 - ый резервный элемент, работает 2-ой резервный элемент, (m - 2) резервных элементов исправны и находятся в режиме недогрузки.
Si- отказал i- й резервный элемент, работает i- й резервный элемент, (m- i) резервных элементов исправны и находятся в режиме недогрузки.
Sm- отказал (m- 1) - ый элемент, работает m- ый резервный элемент.
Sm+1- отказал m-ый резервный элемент.
Запишем систему дифференциальных уравнений Колмогорова. Для этого введём обозначения:
P0(t) - вероятность нахождения резервированной системы в момент времени tв состоянии S0.
Pi(t) - вероятность нахождения резервированной системы в момент времени tв состоянии Si, i= 0, 1,… m, m+ 1.
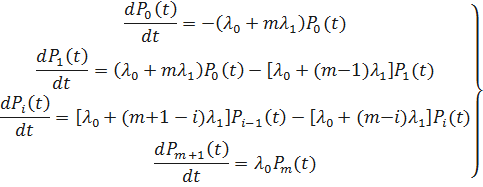
Начальные условия:
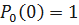
 .
.
Применим к системе дифференциальных уравнений Колмогорова преобразования Лапласа. Получим систему линейных алгебраических уравнений вида: Pi(t) – оригинал
Pi(S) – изображение по Лапласу
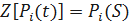 .
.
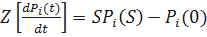 ,
, 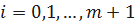
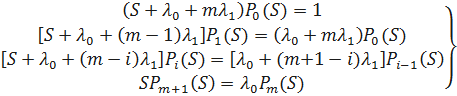
Решая систему уравнений получим
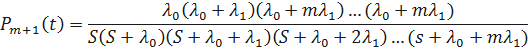
Найдём оригинал 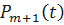 . Имеем
. Имеем
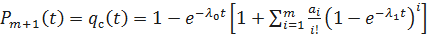 ;
;
где 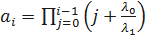 .
.
Здесь 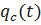 – вероятность отказа резервированной системы с облегчённым резервированием.
– вероятность отказа резервированной системы с облегчённым резервированием.
Определим вероятность безотказной работы системы с облегченным резервированием. Имеем:
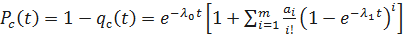 ;
;
Определим среднее время безотказной работы системы с облегченным резервированием. Имеем:
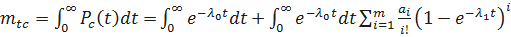 .
.
Формула бинома Ньютона
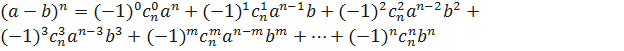 .
.
где 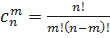
При 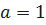 имеем:
имеем:
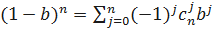 ;
;
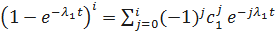 ;
;
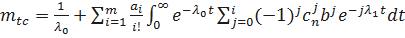 .
.
Выполнив преобразования, получим:
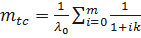 ; где
; где 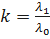 .
.
Определим частоту отказов 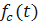 резервированной системы. Имеем
резервированной системы. Имеем
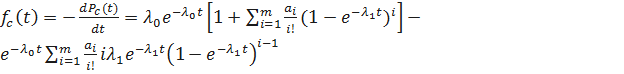 ;
;
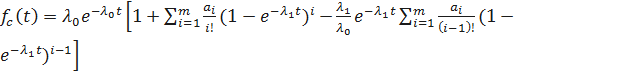 ;
;
Определим интенсивность отказов 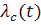 резервированной системы. Имеем
резервированной системы. Имеем
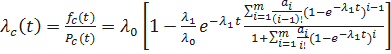 ;
;
Дата добавления: 2015-08-11; просмотров: 2259;
