Режим ненагруженного резерва

При 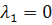имеем режим ненагруженного резерва.

В этом случае

;

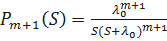Найдём оригинал 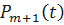. Имеем

;

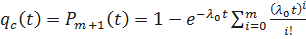Определим вероятность безотказной работы системы с ненагруженным резервом. Имеем:

;

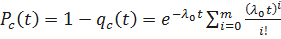Определим время безотказной работы системы с ненагруженным резервом.

;

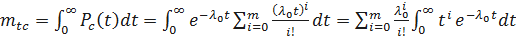где - эйлеров интеграл второго рода.

Известно, что .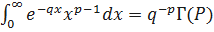

Тогда ;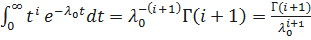

;

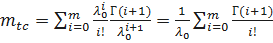Для гамма – функции справедливы соотношения

; .

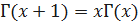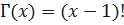Следовательно

; .

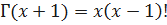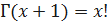Тогда ;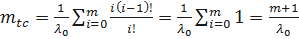

;

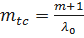Получим формулу для частоты отказов 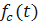. Имеем

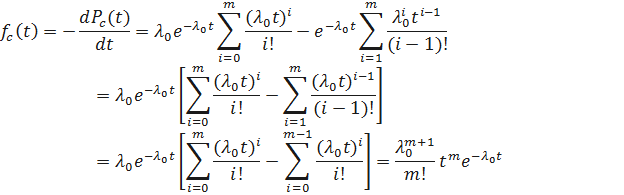
Таким образом ;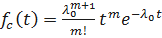

Определим интенсивность отказов 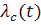. Имеем

; или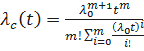

1.25 Основные количественные характеристики надёжности при поэлементном резервировании замещением

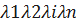
Здесь n – число элементов основной (резервируемой) системы; m – кратность резервирования; 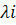– интенсивность отказов элемента i-го типа основной системы.

Вероятность безотказной работы системы вычисляется по формуле

;

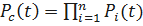где 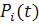- вероятность безотказной работы элемента i – го типа резервированного по способу замещения.

Холодный резерв .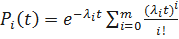

Тёплый резерв ;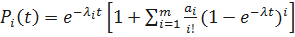

где ;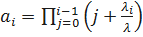

Здесь 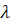– интенсивность отказа резервного элемента i-го типа в режиме недозагрузки до момента включения его в работу:

Холодный резерв ;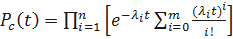

Тёплый резерв .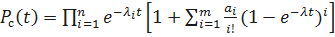

1.26 Анализ надёжности систем при резервировании с дробной кратностью и постоянно включенным резервом

Определим количественные характеристики надёжности при постоянно включенном резерве. Резервированная система состоит из 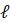отдельных систем. Для её нормальной работы необходимо, чтобы исправными были не менее чем h систем. Кратность 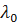резервирования такой системы равна:

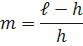
Допущения:

1) Отказы элементов удовлетворяют условиям простейшего потока случайных событий;

2) Переключающие устройства идеальны.

3) Основные и все резервные системы равнонадёжны.

Эти допущения означают, что для любой отдельно взятой системысправедлив экспоненциальный закон надёжности, причём все резервные

элементы находятся в рабочем состоянии с момента включениярезервированной системы в работу.

Резервированная указанным способом система будет работатьнормально при следующих возможных ситуациях:

- ни одна из систем не отказала

- отказала одна система

- отказали две системы

- отказали 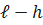систем

Принимая указанные ситуации за гипотезы, вероятность безотказной работы можно записать в виде ;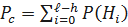

где 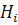– гипотезе, заключающаяся в том, что резервированная система работает исправно при отказе i – любых систем; - вероятность появления гипотезы 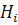; 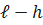- число резервных систем.

Отказы отдельных систем являются событиями независимыми, происходящими при одинаковых условиях работы отдельных систем. В этом случае к приведённым гипотезам применима частная теорема о повторении опытов, и вероятности гипотез подчинены биномиальному распределению:

; ,

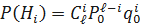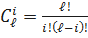где P₀ – вероятность безотказной работы одной системы; q₀–вероятность отказа одной системы.

Подставляя, получим

.

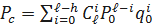Так как

,

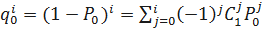то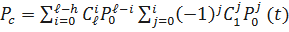

Или ,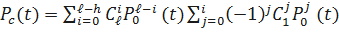

где 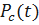- вероятность безотказной работы резервированной системы.

При принятых допущениях ,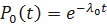

где 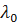- интенсивность отказов любой одной из 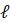систем.

Определим среднее время безотказной работы системы.

Имеем:

.

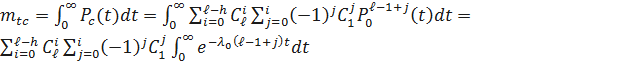Введём обозначение

.

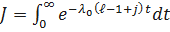Определим J. Имеем:

.

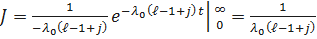Тогда выражение для определения .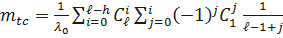

Или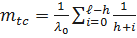

Получим выражение частоты отказов 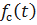. Имеем

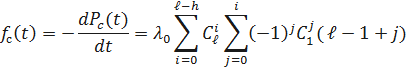
Получим выражение интенсивности отказов системы 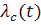. Имеем

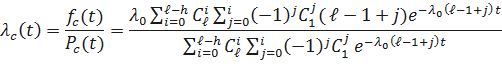
2. НАДЁЖНОСТЬ РЕМОНТИРУЕМЫХ (ВОССТАНАВЛИВАЕМЫХ)

ИЗДЕЛИЙ

2.1 Надёжность системы с восстановлением

Восстанавливаемую систему целесообразно рассматривать как систему массового обслуживания, в которой поток заявок на обслуживание представляет собой поток отказов аппаратуры. Каналами обслуживания являются ремонтные бригады, восстанавливающие работоспособность аппаратуры.

Будем считать, что поток заявок на обслуживание - пуассоновский.

Поток восстановлений - также пуассоновский.

В этом случае для анализа надёжности восстанавливаемой системы можно использовать теорию марковских случайных процессов.

Имеем нерезервированную восстанавливаемую систему, состоящую из одного элемента. Система находится под действием пуассоновского потока отказов с интенсивностью λ. После отказа система начинает немедленно восстанавливаться (ремонтироваться). Поток восстановлений пуассоновский с интенсивностью µ.

В любой момент времени система может находиться в одном из двух состояний:

S₀ - состояние работоспособности,

S₁- состояние отказа (ремонта),

P₀(t)- вероятность нахождения системы в состоянии S₀,

P₁(t) - вероятность нахождения системы в состоянии S₁.

Требуется определить функцию готовности k_г(t) и функцию простоя k_п(t) нерезервированной восстанавливаемой системы.

Функция готовности совпадает с вероятностью работоспособного состояния, т.е.

K_г(t) = P₀(t)

Функция простоя совпадает с вероятностью отказа, т.е.

K_п(t)=P₁(t)

Составим систему дифференциальных уравнений Колмогорова. Имеем

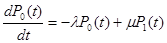
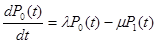
Предположим, что при t= 0 система находилась в работоспособном

состоянии, т.е.

Р₀(0) = 1;

P₁(О) = 0;

Для любого момента времени tимеем

P₀(t) + P₁(t) = l

Из двух уравнений одно является лишним, т.к. P₀(t) иP₁(t) связаны соотношением. Учитывая это, отбросим второе уравнение, а в первое уравнение вместоP₁(t) подставим 1 -P₀(t). Имеем:

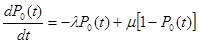
или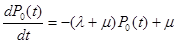

Будем искать решение уравнения при ненулевых начальных условиях. Запишем решение уравнения (2.3). Имеем:

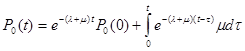
или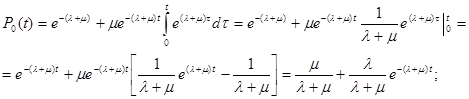

Таким образом

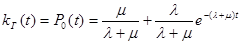
Определим 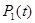.Имеем: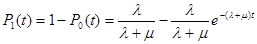

Таким образом:

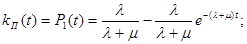
При длительной эксплуатации, т.е. при 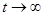имеем:

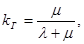
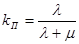
где 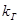- коэффициент готовности системы, 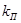- коэффициент простоя системы.

Учитывая, что

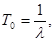
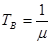
где 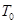- среднее время безотказной работы системы;

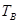- среднее время восстановления (ремонта) системы,

имеем

,

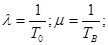
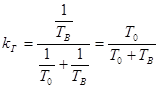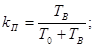
Таким образом, коэффициент готовности характеризует долю времени, в течении которого система работоспособна. Коэффициент простоя характеризует долю времени, в течении которого система ремонтируется.

Определим коэффициент готовности и коэффициент простоя системы, содержащей основной и 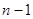резервных элементов, находящихся в нагруженном режиме. Отказавшие элементы образуют очередь на ремонт, который, осуществляется одной бригадой с интенсивностью 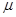.Интенсивность отказа любого элемента равна .

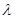Введём в рассмотрение состояния :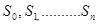

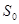-работоспособны все n элементов

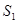- отказал один элемент, остальные работоспособны

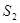- отказали два элемента, остальные исправны

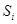- отказали iэлементов, остальные исправны

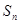- отказала вся система, т.е. отказали все п элементов.

Построим граф состояния системы.

Составим систему дифференциальных уравнений Колмогорова. Имеем:

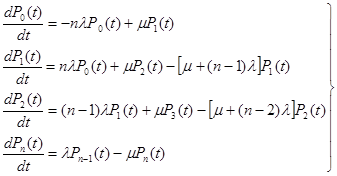
где 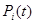- вероятность нахождения системы в момент времени tв состоянии 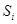= 0,1..., n

В установившемся режиме имеем:

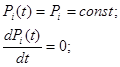
В результате получим систему алгебраических уравнений вида:

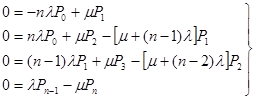
Из системы алгебраических уравнений имеем:

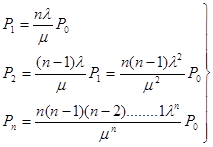
Для вероятностей состояний справедливо следующее соотношение

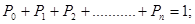
Определим 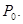Имеем:

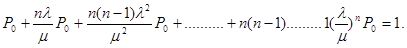
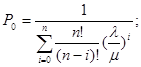
или ;

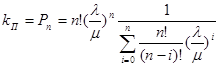Отсюда

Коэффициент готовности:

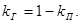
3. НАДЁЖНОСТЬ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ

Исследования в области программной надёжности находятся на начальном этапе своего развития.

Целесообразно выделить две стороны программного обеспечения объекта: программную надёжность объекта - свойство объекта выполнять заданные функции, обусловленные качеством программного обеспечения; надёжность программного обеспечения - свойство программного обеспечения выполнять предписанные ему требования.

Программная надёжность изделия проявляется при совместной работе аппаратуры и программы. Она характеризует способность изделия выполнять заданные функции при условии, что программа будет находиться в том или другом состоянии.

Надёжность программного обеспечения характеризует качественное состояние программы. Её иногда называют правильностью программы, корректностью программы, надёжностью программы.

Программная надёжность объекта - это то, что интересует его потребителя. Для её обеспечения необходимо, чтобы программа была "правильной", "корректной", "надёжной", т.е. чтобы она не содержала ошибок. Может оказаться, что некоторые из ошибок совсем не проявятся при работе объекта или, наоборот, при работе объекта обнаружатся дополнительные несовершенства ("ошибки") программы. Однако очевидно, что необходимым условием надёжной работы объекта является "корректность" программ, т.е. отсутствие в них ошибок.

Программная надёжность становится особо актуальной, когда программы являются самостоятельным изделием.В этом случае они изготовляются, проверяются и подвергаются приёмосдаточным испытаниям так же, как обычные объекты.

Положения о двух сторонах надёжности программного обеспечения полезно иметь в виду при исследовании надёжности программно- управляемых объектов.