Оценка устойчивости электромагнитных систем к воздействию ЭМИ
Исследуя устойчивость работы электромагнитной системы в условиях действия импульсных ЭМП, целесообразно предварительно оценить энергию поля, поглощенную системой. Это особенно важно в случае принципиальной возможности ложных срабатываний устройств при воздействии помехонесущего поля.
Сущность оценки устойчивости систем к воздействию электромагнитного импульса (ЭМИ) сводятся прежде всего к определению механизмов и уровней повреждения элементов, из которых состоит система. Вывод о потенциальной опасности воздействия ЭМИ на систему может быть сделан из сопоставления количества поглощенной энергии ЭМИ с минимальным ее количеством, достаточным для сбоя в работе или необратимых повреждений различных элементов системы [3].
Проведенный таким образом анализ устойчивости системы к воздействию ЭМИ позволит выявить наиболее слабые элементы системы, которые и будут, по сути дела, определять устойчивость всей системы в целом. Повышая устойчивость наиболее слабых элементов системы к воздействию ЭМИ, можно значительно повысить устойчивость системы в целом.
Наиболее эффективными приемниками энергии ЭМИ являются провода, выполняющие роль соединительных линий. Линейные проводники по отношению к помехонесущему полю играют роль электрических антенн и являются приемниками электрического поля; проводники образуют замкнутые контуры, играют роль магнитных антенн и являются приемниками магнитного поля. Оба этих типа приемников являются генераторами ЭДС, которые поглощают часть энергии помехонесущего поля и передают ее соединенным с ними функциональным элементам схем. В таблицах 5.1 ÷ 5.5 приведены ориентировочные значения параметров соединительных проводов.
Исходя из вышесказанного, рекомендуется следующий порядок оценки устойчивости электронных систем к воздействию ЭМИ.
1. Провести анализ элементов электронной системы, выделить основные приемники энергии ЭМИ, контуры, линии проводников.
2. Найти ЭДС, которые наводятся в каждом из этих приемников.
3. Составить эквивалентные схемы, включающие цепи приема энергии и сопротивления, составляющие цепи элементов.
4. Найти токи, напряжения, выделяющуюся в элементах энергию ЭМИ.
5. Сравнить энергию, выделяющуюся в каждом элементе системы, с критическими ее значениями, при достижении которых происходит нарушение функционирования (данные о минимальной энергии, вызывающей сбои в работе или функциональные повреждения элементов электронной аппаратуры, приведены в таблицы 5.6 и 5.2).
Если энергия срабатывания оказывается больше поглощенной энергии поля, то система потенциально устойчива. В противном случае, система потенциально неустойчива и необходимо принятие меры по увеличению ее устойчивости.
Оценка энергии электромагнитного поля, поглощенной в системе, является сложной задачей. Приближенно она может быть решена для случаев взаимодействия поля с проводящими оболочками простых геометрических форм, внутри которых может располагаться аппаратура. Рассмотрим энергию электрического и магнитного поля, поглощенную системой, конструктивно выполненной в проводящем корпусе цилиндрической формы. Изложенный подход может быть распространен и на другие геометрические формы.
Сначала найдем энергию электрического поля, поглощенную системой. В случае, когда длина волны воздействующего электромагнитного поля гораздо больше размеров корпуса системы (а в случае ЭМИ – это безусловно так), последний можно рассматривать как длинноволновую антенну, электрическую – для электрического поля и магнитную – для магнитного поля.
Таблица 5.1 Сопротивление и индуктивность медного прямого провода
| Диаметр провода, мм | Сопротивление при длине 100 мм, Ом | Индуктивность, мкГн, при длине провода, мм | ||
| 0,1 | 0,22 | 0,07 | 0,15 | 0,33 |
| 0,5 | 0,0089 | 0,05 | 0,12 | 0,26 |
| 1,0 | 0,0023 | 0,04 | 0,10 | 0,23 |
| 2,0 | 0,00056 | 0,035 | 0,08 | 0,20 |
Таблица 5.2. Индуктивность, мкГн, на 100 мм медного прямого провода параллельного корпуса прибора
| Диаметр провода, мм | Расстояние между проводом и корпусом, мм | ||
| 0,1 | 0,074 | 0,116 | 0,142 |
| 0,5 | 0,041 | 0,084 | 0,110 |
| 1,0 | 0,028 | 0,028 | 0,096 |
| 2,0 | 0,014 | 0,014 | 0,080 |
Таблица 5.3. Емкость провода, пФ, параллельного корпуса прибора, на 100 мм длины
| Диаметр провода, мм | Расстояние между проводом и корпусом, мм | ||
| 0,1 | 1,5 | 0,9 | 0,7 |
| 0,5 | 2,7 | 1,4 | 0,8 |
| 1,0 | 4,0 | 1,6 | 0,9 |
| 2,0 | 8,0 | 1,8 | 1,0 |
Таблица 5.4. Емкость между двумя параллельными проводами на 100 мм длины, пФ
| Диаметр провода, мм | Расстояние между проводом и корпусом, мм | ||
| 0,1 | 0,75 | 0,5 | 0,04 |
| 0,5 | 1,4 | 0,75 | 0,05 |
| 1,0 | 2,0 | 0,9 | 0,06 |
| 2,0 | 5,0 | 1,3 | 0,07 |
Таблица 5.5. Взаимоиндуктивность между двумя параллельными проводами одной длины, мкГН
| Диаметр провода, мм | Расстояние между проводом и корпусом, мм | ||
| 0,03 | 0,015 | 0,008 | |
| 0,07 | 0,04 | 0,024 | |
| 0,17 | 0,11 | 0,07 |
Таблица 5.6. Минимальная энергия, вызывающая функциональные повреждения элементов электронной аппаратуры и воспламенение пиротехнических устройств
| № | Наименование элемента | Минимальная энергия, Дж |
| Низкочастотный транзистор (германиевый) | 4·10–2 | |
| Переключающие транзисторы n-p-n | 6·10–5 | |
| Переключающие транзисторы p-n-p | 8·10–4 |
Продолжение таблицы 5.6
| Интегральная схема (кремневая) | 8·10–5 | |
| Туннельный диод | 5·10–4 | |
| Высокочастотный диод (кремневый) | 1·10–7 | |
| Управляемый выпрямитель (кремневый) | 3·10–3 | |
| Вариатор (германиевый) | 1·10–4 | |
| Электронная лампа СВЧ | 1·100 | |
| Реле слабого тока | 2·10–3 | |
| Реле (на 1 А) | 1·10–1 | |
| Микроамперметр | 3·10–3 | |
| Разрывной болт | 6·10–4 | |
| Запал | 2·10–5 | |
| Пары топлива | 3·10–3 |
Таблица 5.7. Минимальная энергия, Дж, вызывающая сбои в работе электронных систем
| Вид устройства | Минимальная энергия | Характер сбоя | Дополнительные данные |
| Плата с логическими элементами | 3·10–9 | Сбой работы схемы | Типичный резисторно- транзисторный логический ключ |
| Плата с логическими элементами | 1·10–9 | Сбой работы схемы | Типичная триггерная схема на транзисторах |
| Интегральная схема | 4·10–10 | Сбой работы схемы | Монолитная тригерно- интегрирующая схема |
| Устройство оперативной памяти | 2·10–9 | Стирание записи | Запоминающее устройство на магнитных сердечниках |
| Оперативная память | 3 – 5·10–9 | Стирание записи | Запоминающее устройство на магнитных сердечниках |
| Усилитель | 4·10–21 | Помехи | Типичный усилитель с большим коэффициентом усиления |
Угольные резисторы способны выдерживать импульсные мощности, более чем в 10 000 раз превышающие их собственную номинальную мощность. Конденсаторы также относятся к числу довольно стойких к импульсному воздействию элементов.
Минимальная энергия, необходимая для того, чтобы произошел сбой в работе электронной или электрической системы, примерно на 1 – 2 порядка меньше энергии, вызывающей необратимые изменения.
При рассмотрении сечения герметичной проводящей цилиндрической оболочки радиуса r0 и длиной l , находящейся в продольном электрическом поле E0.
Под действием электрического поля цилиндр поляризуется и на каждом из его оснований индуцируется заряд

где ε0 – диэлектрическая проницаемость.
При изменении во времени электрического поля заряды также изменяются во времени и на боковой поверхности оболочки протекает ток. Этот ток связан с разделением электрических зарядов и замыкается вне цилиндра токами смещения.
Следовательно, по отношению к воздействующему полю проводящий корпус системы с точки зрения введенного в нем тока ведет себя как емкость, включенная последовательно с омическим сопротивлением проводника, т.е. проводящий корпус системы в электрическом поле можно рассматривать как короткую электрическую антенну.
Эквивалентная схема для расчета тока в оболочке системы совпадает с эквивалентной схемой цепи короткой электрической антенны. Омическое сопротивление оболочки цилиндрической формы, имеющей стенки толщиной d с проводимостью σ равно

Емкость оболочки находится из соотношения (5.1), если учесть, что q = C0v , где v = E0l – разность потенциалов оснований цилиндра. Отсюда
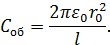
Энергия электрического поля, поглощенного системой, равна
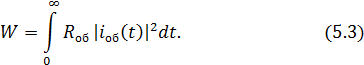
Ток оболочки iоб(t) может быть найден из выражения
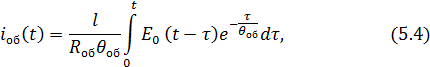
где 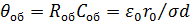 – постоянная времени оболочки.
– постоянная времени оболочки.
Подставляя (5.4) в (5.3), найдем энергию электрического поля, поглощенную системой:
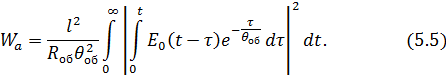
В случае действия магнитного поля, индуцированные токи протекают по периметру сечения, перпендикулярного направлению вектора магнитного поля.
Меняющееся во времени магнитное поле индуцирует в таком короткозамкнутом витке ЭДС, которая пропорциональна скорости изменения магнитного поля. При очень низких частотах ток в витке пропорционален приложенной ЭДС, деленной на омическое сопротивление витка. Этот ток сдвинут на π/2 относительно приложенного помехонесущего поля.
Когда скорость изменения приложенного поля увеличивается, индуктивное сопротивление проводника растет и становится гораздо больше его омического сопротивления. Таким образом, по отношению к магнитному полю проводящий корпус системы с точки зрения наведенного в нем тока ведет себя как индуктивность, включенная последовательно с омическим сопротивлением, определяемым собственным омическим сопротивлением оболочки, т.е. проводящий корпус системы в магнитном поле можно рассматривать как короткозамкнутый виток, или магнитную антенну.
Эквивалентная схема для расчета тока в оболочке системы, возникающего под действием магнитного поля, совпадает с эквивалентной схемой цепи рамочной антенны.
Определим индуктивность оболочки Lоб для протекающего по ее периметру поперечного кругового тока. Если этот ток обозначить iоб, а ЭДС, самоиндукции в оболочке εоб, то

Ток в оболочке создает магнитное поле H , которое может быть найдено по закону полного тока

где dl – дифференциал длины кривой, ограничивающей сечение S, через которое протекает ток оболочки;
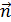 – единичный вектор (орт) нормали к поверхности S.
– единичный вектор (орт) нормали к поверхности S.
Если рассмотреть продольное сечение цилиндрической оболочки, направления линий тока и контур интегрирования ABCD, охватывающий ток iоб, закон полного тока в этом случае дает

ЭДС самоиндукции определяется из второго закона Максвелла:
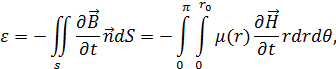
где B – магнитная индукция;
μ – магнитная проницаемость среды.
Будем считать, что напряженность магнитного поля постоянна по сечению оболочки. Учитывая, что d << r, после интегрирования получим
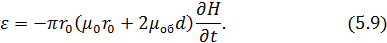
Здесь через μ0 обозначена магнитная проницаемость среды, заполняющей полость оболочки (для воздуха μ0 = 4π10-7 Гн/м). Из (5.6), (5.8) и (5.9) найдем индуктивность оболочки для поперечного кругового тока:
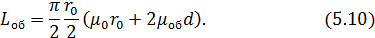
Энергия магнитного поля поглощенная системой
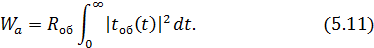
Если действует импульс магнитного поля прямоугольной формы длительностью tn и амплитудой Hm, то индуцируемая в оболочке ЭДС в соответствии с (5.9) будет:
 .
.
где δ(t) – дельта-функция (единичная импульсная функция).
Соответственно ток оболочки равен:
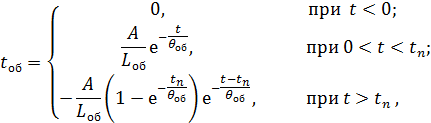
где
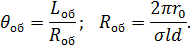
Подставляя найденный ток в выражение для поглощенной энергии (5.11), получим
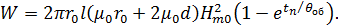
Сравнивая поглощенную энергию ЭМИ элементами и схемами электронной системы с минимальным уровнем энергии, достаточной для сбоя в работе или необратимых повреждений, можно сделать вывод об устойчивости отдельных элементов и системы в целом к воздействию ЭМИ.
Приведенная методика оценки устойчивости электронных систем к воздействию ЭМИ ядерного взрыва может быть выполнена при условии знания величин напряженностей электрического, магнитного полей ЭМИ в области пространства, где размещены исследуемые системы. В условиях мирного времени можно лишь предположительно судить об этих величинах.
Поэтому для оценки устойчивости различной электронной аппаратуры к воздействию ЭМИ можно использовать более упрощенную схему оценки.
Порядок проведения оценки в этом случае может быть следующим.
1. Составить перечень основных комплектующих элементов анализируемой аппаратуры.
2. Приближенно определить степень защищенности K от ЭМИ для каждого элемента схемы (наличие приемников ЭМИ, проводников, связанных с данным элементом, экранов, фильтров, заземлений и т.д.). Величина K может быть как больше единицы, так и меньше единицы.
3. Используя таблицы 5.6 и 5.7, а также литературные данные по минимальной энергии ЭМИ, вызывающей повреждения или сбои в работе рассматриваемых элементов, и выявленную степень их защищенности в конструктивной схеме и конструкции, определить наименее стойкие к воздействию ЭМИ элементы.
4. Выработать предложения по повышению устойчивости наименее устойчивых элементов с целью повысить устойчивость всей аппаратуры (системы) в целом, используя один из методов, описанных ниже.
5. После повышения устойчивости системы обратным расчетом, рекомендуемым в данном параграфе, определить значения напряженностей ЭМП, создаваемого ЭМИ, которые не вызовут нарушения функционирования оцениваемой системы.
Дата добавления: 2015-08-11; просмотров: 3626;
