Занятие №38. Задачи, приводящие к дифференциальным уравнениям
№1. Записать уравнение кривой, проходящей через точку 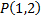 и обладающей следующим свойством: площадь треугольника, образованного радиус–вектором любой точки кривой, касательной в этой точке и осью абсцисс, равна 2.
и обладающей следующим свойством: площадь треугольника, образованного радиус–вектором любой точки кривой, касательной в этой точке и осью абсцисс, равна 2.
Примечание: Сделаем чертеж (рис. 80).
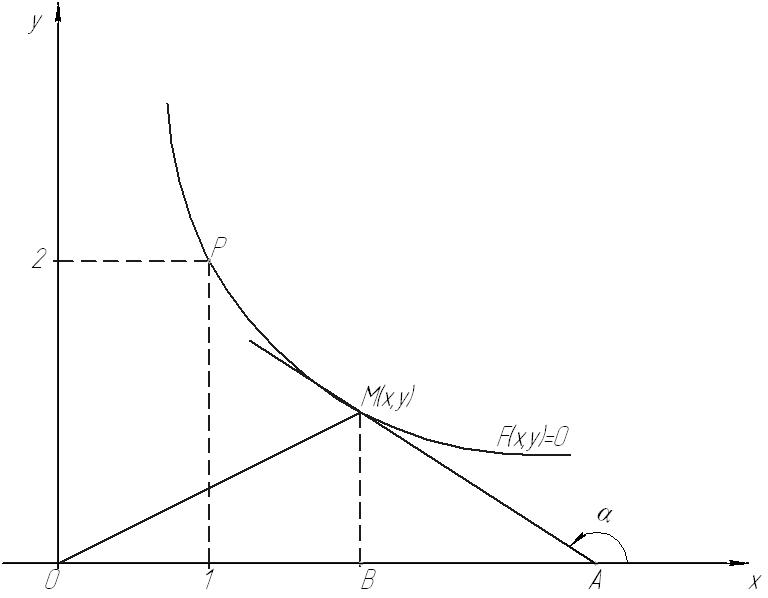
Рис. 80
Из рисунка видно,
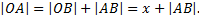
Из треугольника 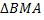 получаем
получаем
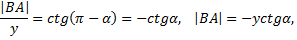
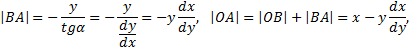
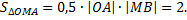
Подставляя в последнее равенство выражения для 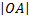 и
и 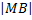 , приходим к дифференциальному уравнению
, приходим к дифференциальному уравнению
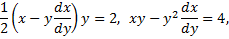
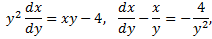
т.е. получили уравнение первого порядка, линейное относительно функции 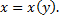 Решаем его с помощью подстановки
Решаем его с помощью подстановки  Имеем
Имеем
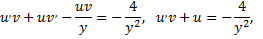

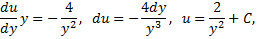
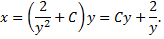
Искомая кривая проходит через точку 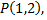 поэтому
поэтому 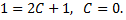 Следовательно, ее уравнение
Следовательно, ее уравнение 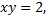 т.е. данная кривая гипербола.
т.е. данная кривая гипербола.
№2. Записать уравнение кривой, если известно, что точка пересечения любой касательной к кривой с осью абсцисс одинаково удалена от точки касания и от начала координат.
Примечание: 
№3. Записать уравнение кривой, если известно, что расстояние от любой касательной до начала координат равно абсциссе точки касания.
Примечание: 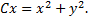
№4. Записать уравнение кривой, проходящей через точку 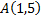 и обладающей следующим свойством: длина отрезка, отсекаемого на оси ординат любой касательной, равна утроенной абсциссе точки касания.
и обладающей следующим свойством: длина отрезка, отсекаемого на оси ординат любой касательной, равна утроенной абсциссе точки касания.
Примечание: 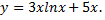
№5. Записать уравнение кривой, проходящей через точку 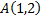 и обладающей следующим свойством: отношение ординаты любой ее точки к абсциссе этой точки пропорционально угловому коэффициенту касательной к искомой кривой, проведенной в той же точке. Коэффициент пропорциональности равен 3.
и обладающей следующим свойством: отношение ординаты любой ее точки к абсциссе этой точки пропорционально угловому коэффициенту касательной к искомой кривой, проведенной в той же точке. Коэффициент пропорциональности равен 3.
Примечание: 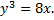
Дата добавления: 2015-08-11; просмотров: 2952;
