Методы обработки экспертной информации

Экспертное ранжирование. Рангом называется степень отличия по какому-либо признаку, а ранжированием - процесс определения рангов, относительных количественных оценок степеней отличий по качественным признакам (например, расположение факторов в порядке их существенности, значимости в данном исследовательском контексте).

Ранжирование применяется в случаях, когда невозможна или нецелесообразна непосредственная оценка. При этом ранжирование объектов содержит лишь информацию о том, какой из объектов более предпочтителен, и не содержит информацию о том, насколько или во сколько раз один объект предпочтительнее другого. Объект, расположенный в ранжировании эксперта, скажем, на третьем месте, может превосходить объект, расположенный на четвертом месте, в 1,01 раза, а может превосходить и в 101 раз.

Метод простой ранжировки заключается в том, что эксперты располагают объекты ранжирования (например, критерии) в порядке убывания их значимости (для альтернатив это убывание предпочтительности). Ранги обозначаются цифрами от 1 до n, где n — количество рангов. Сумма рангов Sn при этом будет равна сумме чисел натурального ряда:

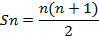
Так, при n=6последовательность рангов альтернатив An может выглядеть следующим образом: 2, 4, 1, 3, 6, 5, что означает, что ранг альтернативы Aз равен единице (R_a3=1) и она наиболее предпочтительна из всех шести альтернатив (наименее предпочтительнаальтернатива A₅, так как R_a5=6).

При ранжировании n объектов m экспертам ранжирование проводят следующим образом.

1. Каждый эксперт выносит суждения о рангах объектов.

2. Для каждого объекта подсчитывают сумму рангов, полученных от всех экспертов, т.е.

,

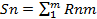Где Sn – представляет собой результирующий ранг n- объекта;

R_Anm - суждение m-го эксперта о ранге n-го объекта.

3. Определяют ранги объектов (от 1-го до п), начиная от наименьшего до наибольшего результирующего рангов.

Метод непосредственной оценки заключается в отнесении объекта оценки к определенному значению по оценочной шкале (т.е. в присвоении объекту оценки балла в определенном интервале). Например, оценка от 0 до 10 в соответствии с предпочтением по какому-либо признаку или их группе (например, альтернативы, по предпочтению, критерии - по значимости, факторы внешней среды - по оказываемому влиянию, проблемы — по приоритетности решения).

Для дальнейшей обработки полученные оценки могут быть пронормированы, т.е. их сумма может быть приведена к единице путем деления каждой оценки на их общую сумму.

Для наглядности и удобства обработки (например, осуществление выбора ЛПР) оценки могут быть переведены в ранги. Максимальной оценке при этом соответствует наивысший ранг, т.е. 1, а минимальной - п (при п - количестве объектов оценки).

При оценке объекта по нескольким параметрам (например, при оценке альтернатив по нескольким критериям) суммарная оценка объекта проводится следующим образом.

1. Эксперты выносят суждения о весах параметров (например, о весах критериев) и оценках объекта по множеству параметров (например, оценки альтернатив по критериям).

2. Аналитики обрабатывают полученные оценки: вычисляют Нормализованные веса параметров (например, критериев) по формулам арифметического среднего, геометрического среднего или средневзвешенного. Так, методом вычисления средних арифметических веса находятся следующим образом:

§ нормализуют оценки весов параметров отдельно по каждому эксперту (табл. 8.3, стр. 2—4)

§ находят средние арифметические весов параметров (см. строку 5 таб.8.3);

§ подсчитывают оценки объектов по параметрам, вычисляемым аналогично вычислению весов параметров, и определяют комплексные оценки объектов по следующей формуле:

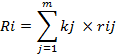
Где Ri –комплексная оценка i-го объекта (i=1….n, где n –количество объектов оценки);

k_j – нормализованный весовой коэффициент j -го параметра;

r_{ij –} нормализованная оценка i-го объекта по j- му параметру;

m - количество параметров.

Затем комплексные оценки нормализуют.

Таблица 8.3