Тема 11. Уравнение состояния идеального газа.

Состояние системы задаетсятермодинамическими параметрами – совокупностью физических величин, характеризующих свойства термодинамической системы, например, давлением р, объемом V и температурой Т. Между этими параметрами существует определенная связь, называемаяуравнением состояния, которое имеет общий вид:

,

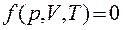где каждая из переменных является функцией двух других.

Для идеального газа уравнением состояния является уравнение Клапейрона – Менделеева:

,

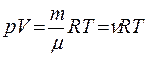где m – масса газа, 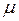– молярная масса (масса одного моля вещества),

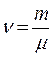– количество вещества,

R – универсальная газовая постоянная, .

(Идеальнымназывается такой газ, в котором считается, что собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда, в котором он находится, силы взаимодействия между молекулами газа отсутствуют, а столкновения между молекулами газа абсолютно упругие.)

Исходя из уравнения Клапейрона – Менделеева и понятия концентрации n (n – число молекул в единице объема: 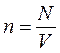, где N – число всех молекул газа), можно получить уравнение состояния идеального газа в ином виде:

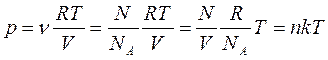, то есть ,

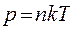где 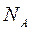– постоянная Авогадро – число молекул в одном моле вещества,

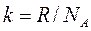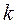, – постоянная Больцмана.