Определение осадок линейно-деформируемого полупространства или слоя грунта ограниченной мощности.
Используются строгие решения о распределении напряжений в однородном изотропном массиве грунтов от нагрузок, приложенных на его поверхности. Зависимость между осадкой подошвы центрально-нагруженного фундамента s, площадью фундамента A=bl, и средним значением дополнительного давления p0=p-γd имеет вид:
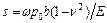 , ,
| (1) |
где ω – коэф., зависит от формы площади и жесткости фундамента, ν, Е – коэф. Пуассона и модуль деформации грунта основания.
Данное решение применимо только для однородного напластования грунтов на значительную глубину ниже подошвы фундамента. Не учитывается изменение природного напряженного состояния грунтов основания с глубиной, при значительных размерах фундаментов расчётные значения осадок завышенные. Решение используется при небольших размерах фундаментов на однородных основаниях и для определения модуля деформации по данным опытов с пробной нагрузкой.
5.1.3. Основные предпосылки приближенных методов расчёта осадок.
Осадка грунта происходит только в пределах глубины сжимаемой толщи Нс. Осадка основания происходит только за счёт сжатия столба грунта, непосредственно находящегося под подошвой фундамента (рис. 5.2, а). Сжатие каждого элементарного слоя мощностью Δz вызывается равномерно распределенной на его поверхности нагрузкой равной максимальному значению σzp, действующему по оси z.
Определив величину сжатия каждого элементарного слоя грунта в пределах сжимаемой толщи основания и просуммировав эти величины, получим общую осадку основания фундамента. Такой подход к решению задачи называют методом послойного (элементарного) суммирования.
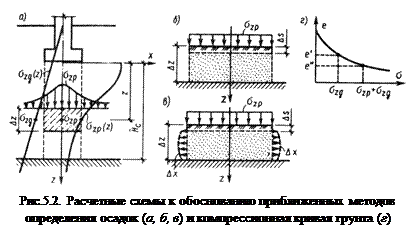 Возможны два расчётных случая: сжатие элементарного слоя без бокового расширения (рис. 5.2, б); сжатие элементарного слоя с возможностью бокового расширения (рис. 5.2, в).
Возможны два расчётных случая: сжатие элементарного слоя без бокового расширения (рис. 5.2, б); сжатие элементарного слоя с возможностью бокового расширения (рис. 5.2, в).
В первом случае:
εx= εy=0.
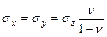 . .
| (5.2) |
Относительная деформация элементарного слоя:
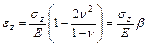 . .
| (5.3) |
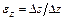 ;
;
Сжатие элементарного слоя
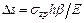 ; ;
| (5.4) |
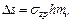 . .
| (5.5) |
Для определения деформационных характеристик грунтов используются компрессионные испытания.
Во втором случае:
εx= εy≠0.
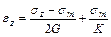 , ,
| (5.6) |
где G – модуль сдвига, K – модуль объемной деформации грунта.
Сжатие элементарного слоя для пространственной задачи:
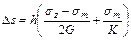 . .
| (5.7) |
Для плоской задачи среднее напряжение определяется по формуле:
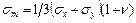 . .
| (5.8) |
Для точного определения деформационных характеристик требуется проведение специальных опытов в приборах трехосного сжатия.
Дата добавления: 2015-08-08; просмотров: 787;
